Two spheres of radii 2 cm and 3 cm are charged to the same potential. If σ and σ2 be respectively the values of surface charge density on the conductors, then the ratio σ1σ2 will be
(a)49
(b)23
(c)32
(d)94
The correct Answer is:C
To solve the problem, we need to find the ratio of surface charge densities (σ1 and σ2) on two spheres of different radii that are charged to the same potential.
1. Understand the relationship between charge density and potential:
The surface charge density (σ) on a sphere is related to its potential (V) and radius (r) by the formula:
σ=QA=V⋅rk⋅A
where A is the surface area of the sphere, A=4πr2.
2. Express charge density in terms of potential and radius:
The potential V of a charged sphere is given by:
V=kQr
Rearranging gives:
Q=V⋅rk
The surface area A of a sphere is 4πr2, so the surface charge density can be expressed as:
σ=QA=V⋅rk⋅4πr2=V4πkr
3. Relate the surface charge densities of the two spheres:
Let σ1 be the surface charge density of the sphere with radius r1=2cm and σ2 be that of the sphere with radius r2=3cm. Since both spheres are at the same potential V:
σ1=V4πkr1andσ2=V4πkr2
4. Calculate the ratio of surface charge densities:
Now, we can find the ratio σ1σ2:
σ1σ2=V4πkr1V4πkr2=r2r1
5. Substitute the values of the radii:
Substitute r1=2cm and r2=3cm:
σ1σ2=32
Final Answer:
The ratio of the surface charge densities σ1σ2 is 32.
The surface charge density (σ) on a sphere is related to its potential (V) and radius (r) by the formula:
σ=QA=V⋅rk⋅A
where A is the surface area of the sphere, A=4πr2.
The potential V of a charged sphere is given by:
V=kQr
Rearranging gives:
Q=V⋅rk
The surface area A of a sphere is 4πr2, so the surface charge density can be expressed as:
σ=QA=V⋅rk⋅4πr2=V4πkr
Let σ1 be the surface charge density of the sphere with radius r1=2cm and σ2 be that of the sphere with radius r2=3cm. Since both spheres are at the same potential V:
σ1=V4πkr1andσ2=V4πkr2
Now, we can find the ratio σ1σ2:
σ1σ2=V4πkr1V4πkr2=r2r1
Substitute r1=2cm and r2=3cm:
σ1σ2=32
The ratio of the surface charge densities σ1σ2 is 32.
Similar Questions
Two spherical conductors of radii 4cmand5cm are charged to the same potential. If σ1andσ2 be respective value of surface density of charge on both the conductors, then the ratio of σ1/σ2 will be
View SolutionTwo isolated metallic spheres of radii 2 cm and 4 cm are given equal charge, then the ratio of charge density on the surfaces of the spheres will be
View Solution
Knowledge Check
- Question 1 - Select One
Two metal wires of identical dimesnios are connected in series. If σ1 and σ2 are the conducties of the metal wires respectively, the effective conductivity of the combination is
Aσ1+σ2Bσ1+σ22C√σ1+σ2D2σ1+σ2σ1+σ2
Electrical conductivies of Ge and Na are σ1 and σ2 respectively. If these substances are heard, then
View SolutionAnswer the following:
(i) If two similar large plates, each of area A having surface charge densities +σ and −σ are separated by a distance d in air,find the expression for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, in which direction will the charge flow and why ?View SolutionTwo concentric spheres of radii R and r have similar charges with equal surface charge densities (σ). The electric potential at their common centre is
View SolutionIf σx=5,r=−12andbyx=−27 , then the value of σy is:
View SolutionThree concentric spherical metal shells A.B.C of radii a,b,c(c>b>a) have surface charge density +σ,−σand+σ respectively. The potential of the middle shell is σε0 times
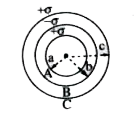 View Solution
View SolutionTwo metal wires of identical dimesnios are connected in series. If σ1 and σ2 are the conducties of the metal wires respectively, the effective conductivity of the combination is
View SolutionThere are three concentric thin spheres of radius a,b,c(a>b>c). The total surface charge densities on their surfaces are σ,−σ,σ respectively. The magnitude of the electric field at r (distance from centre) such that a>r>b is:
View Solution

