The vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jornalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A river is flowing from west to east at a speed of 5 m/s. A man on the south bank of the river, capable of swimming at 10 m/s in still water, wants to cross the river without drifting, he should swim

due north
30∘ east of north
30∘ west of north
60∘ east of north
The correct Answer is:C
Step by step video & image solution for The vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jornalism greatly simplifies many problems. If vecv_(A)is the absolute velocity of a body A and vec_(B)that of another body B then the relative velocity of A in relation to B is vec_(AD)=vecV_(A)-vecv_(B) and vecv_(BA)=vecv_(B)-vecv_(A). The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity Q A river is flowing from west to east at a speed of 5 m/s. A man on the south bank of the river, capable of swimming at 10 m/s in still water, wants to cross the river without drifting, he should swim by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is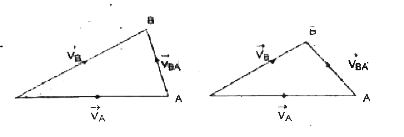
View SolutionVelocity of a body is variable when
View Solution
Knowledge Check
Assertion : The sound emitted by the source travels in all directions.
Reason : The relative velocity of sound with respect to the observer is the sum of velocity of sound and velocity of observer.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
The angular velocity of a rigid body about any point of that body is same :
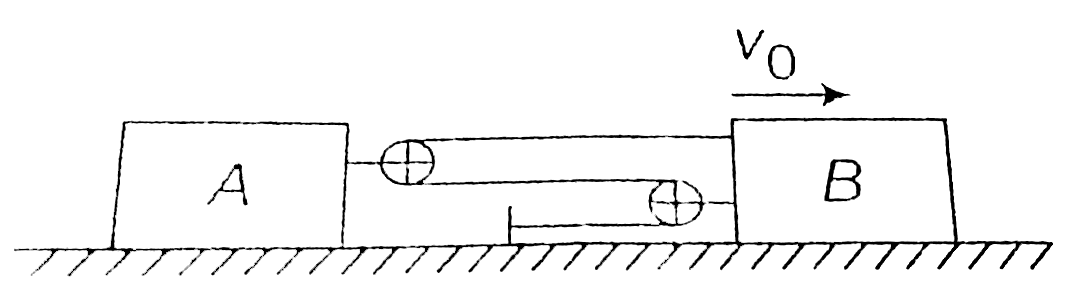
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body a relative to b is
View SolutionProblems on Relative Velocity of Rain and Woman
View SolutionWhat is the average velocity of a body in uniform circular motion ?
View SolutionWhat is meant by relative velocity ? Write an expression for the velocity of A and B particle relative to the other moving with velocities v and v along a straight line.
View SolutionAssertion: The relative velocity of the two particles in head-on elastic collision is unchanged both in magnitude and direction.
Reason: The relative velocity is unchanged in magnitude but gets reversed in direction.
View SolutionAssertion: The relative velocity of the two particles in head-on elastic collision is unchanged both in magnitude and direction.
Reason: The relative velocity is unchanged in magnitude but gets reversed in direction.
View Solution
