Problems on Relative Velocity of Rain and Woman
To solve the problem of the relative velocity of rain and a woman running with an umbrella, we will follow these steps:
1. Understand the Problem:
- The rain is falling vertically downwards with a certain velocity, Vr.
- The woman is running horizontally with a velocity, Vw.
- We need to find the angle θ at which the woman should hold her umbrella so that she does not get wet.
2. Identify the Velocities:
- Let the velocity of rain be Vr (downward).
- Let the velocity of the woman be Vw (horizontal).
3. Draw the Velocity Vectors:
- Draw a vertical vector pointing downwards for the rain's velocity.
- Draw a horizontal vector pointing in the direction of the woman's motion for her velocity.
4. Use the Concept of Relative Velocity:
- The effective direction of the rain relative to the woman can be determined by considering the vector sum of the rain's velocity and the woman's velocity.
- The angle θ with the vertical can be found using the tangent function.
5. Set Up the Relationship:
- From the triangle formed by the velocity vectors, we can write:
tan(θ)=VwVr
6. Solve for the Angle θ:
- To find θ, we take the inverse tangent:
θ=tan−1(VwVr)
7. Conclusion:
- The woman should hold her umbrella at an angle θ given by:
θ=tan−1(VwVr)
- This angle ensures that she is not affected by the rain.
- The rain is falling vertically downwards with a certain velocity, Vr.
- The woman is running horizontally with a velocity, Vw.
- We need to find the angle θ at which the woman should hold her umbrella so that she does not get wet.
- Let the velocity of rain be Vr (downward).
- Let the velocity of the woman be Vw (horizontal).
- Draw a vertical vector pointing downwards for the rain's velocity.
- Draw a horizontal vector pointing in the direction of the woman's motion for her velocity.
- The effective direction of the rain relative to the woman can be determined by considering the vector sum of the rain's velocity and the woman's velocity.
- The angle θ with the vertical can be found using the tangent function.
- From the triangle formed by the velocity vectors, we can write:
tan(θ)=VwVr
- To find θ, we take the inverse tangent:
θ=tan−1(VwVr)
- The woman should hold her umbrella at an angle θ given by:
θ=tan−1(VwVr)
- This angle ensures that she is not affected by the rain.
Similar Questions
A man is walking on a road with a velocity 3kmhr. Suddenly rain starts falling. The velocity of rain is 10km/hr in vertically downward direction. the relative velocity of rain with respect to man is :-
View SolutionAssertion: For inelastic collision, 0≤e<1.
Reason: Hence, the magnitude of relative velocity of separation after collision is less than relative velocity of approach before collision.
View SolutionAssertion: The relative velocity of the two particles in head-on elastic collision is unchanged both in magnitude and direction.
Reason: The relative velocity is unchanged in magnitude but gets reversed in direction.
View SolutionAssertion: The relative velocity of the two particles in head-on elastic collision is unchanged both in magnitude and direction.
Reason: The relative velocity is unchanged in magnitude but gets reversed in direction.
View Solutionf A and B persons are moving with VAandVB. velocities in opposite directions. Magnitude of relative velocity of B w.r.t. A is x and magni-tude of relative velocity of A w.r.t B is y. Then
View SolutionSTATEMENT-1 : In an elastic collision between two bodies, the relative velocity of separation equals relative velocity of approach.
and
STATEMENT-2 : In a elastic collision , the coefficient of restitution is 1.
View SolutionRain is falling vertically with a velocity of 4 km hr−1 . A cyclist is going along a horizontal road with a velocity of 3 km hr−1 towards cast. Calculate the relative velocity of the rain with respect to the cyclist. In what direction must the cyclist hold his umbrella to save himself from the falling rain ?
View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
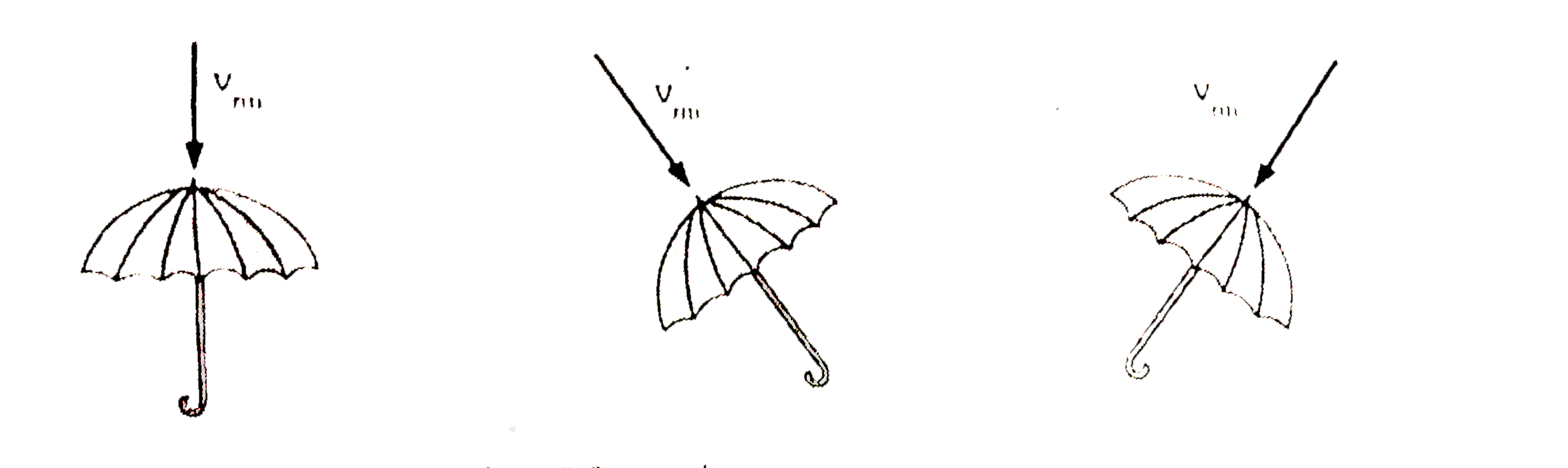
A man walks in rain at 72 cm/m due east and observes the rain falling vertically. When he stops, rain appears to strike his back at 37∘ from the vertical. Find velocity of raindrops relative to the ground.
View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.

When you are standstill in rain, you have to hold umbrella vertically to protect yourself.
(a) When you walk with velocity 90 cm/s, you have to hold your umbrella at 53∘ above the horizontal. What is velocity of the raindrops relative to the ground and relative to you ?
(b) If you walk with speed 160 cm/s, how should you hold your umbrella ?
View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.

Rain is falling vertically with velocity 80 cm/s.
(a) How should you hold your umbrella ?
(b) You start walking towards the east with velocity 60 cm/s. How should you hold umbrella ?
(c) You are walking towards the west with velocity 60 cm/s. How should you hold your umbrella ?
(d) You are walking towards the north with velocity 60 cm/s. How should you hold your umbrella?
(e) You are walking towards the south with velocity 80 cm/s. How should you hold your umbrella ?
View Solution