Statement - 1 : Let I1andI2 be the moment of inertia of two bodies of identical geometrical shapes, the first made of aluminium and second of iron then I1<I2. Becaause
Statement - 2 : Moment of inertia does not depends on shape
Statement - 1 is true, statement - 2 is true, statement - 2 is correct explanation for statement - 1
Statement - 1 is true, Statement - 2 is true, Statement - 2 is not a correct explanation for statement - 1
statement - 1 is true, statement - 2 is false
statement - 1 is false, statement - 2 is true.
The correct Answer is:C
To analyze the given statements and arrive at a conclusion, let's break down the problem step by step.
Step 1: Understanding Moment of Inertia
The moment of inertia (I) of an object is a measure of how difficult it is to change its rotational motion about a particular axis. It depends on both the mass of the object and how that mass is distributed relative to the axis of rotation.
Step 2: Analyzing Statement 1
Statement 1 claims that the moment of inertia of two bodies with identical geometrical shapes, one made of aluminum (I1) and the other made of iron (I2), satisfies the inequality I1 < I2.
- Reasoning:
- Aluminum has a lower density than iron.
- Since both objects have the same shape and size, the mass of the aluminum object will be less than that of the iron object.
- Therefore, the moment of inertia, which is dependent on mass, will also be less for the aluminum object.
Step 3: Analyzing Statement 2
Statement 2 states that the moment of inertia does not depend on shape.
- Reasoning:
- This statement is incorrect. The moment of inertia does depend on the shape of the object because it is influenced by how the mass is distributed with respect to the axis of rotation.
- For example, if the mass is distributed further from the axis, the moment of inertia increases, and if it is closer, the moment of inertia decreases.
Step 4: Conclusion
Based on the analysis:
- Statement 1 is true: I1 < I2 because aluminum has a lower density than iron.
- Statement 2 is false: Moment of inertia does depend on the shape of the object.
Thus, the correct conclusion is that Statement 1 is true and Statement 2 is false.
Final Answer
- Correct Option: Statement 1 is true, Statement 2 is false.
---
The moment of inertia (I) of an object is a measure of how difficult it is to change its rotational motion about a particular axis. It depends on both the mass of the object and how that mass is distributed relative to the axis of rotation.
Statement 1 claims that the moment of inertia of two bodies with identical geometrical shapes, one made of aluminum (I1) and the other made of iron (I2), satisfies the inequality I1 < I2.
- Aluminum has a lower density than iron.
- Since both objects have the same shape and size, the mass of the aluminum object will be less than that of the iron object.
- Therefore, the moment of inertia, which is dependent on mass, will also be less for the aluminum object.
Statement 2 states that the moment of inertia does not depend on shape.
- This statement is incorrect. The moment of inertia does depend on the shape of the object because it is influenced by how the mass is distributed with respect to the axis of rotation.
- For example, if the mass is distributed further from the axis, the moment of inertia increases, and if it is closer, the moment of inertia decreases.
Based on the analysis:
- Statement 1 is true: I1 < I2 because aluminum has a lower density than iron.
- Statement 2 is false: Moment of inertia does depend on the shape of the object.
- Correct Option: Statement 1 is true, Statement 2 is false.
Similar Questions
Knowledge Check
The moments of inertia of two rotating bodies A and B are IA and IB(IA>IB). If their angular momenta are equal then.
Aa. Kinetic energy of A = Kinetic energy of BBb. Kinetic energy of A > Kinetic energy of BCc. Kinetic energy of A < Kinetic energy of BDd. Kinetic energy of the two bodies cannot be compared with the given data
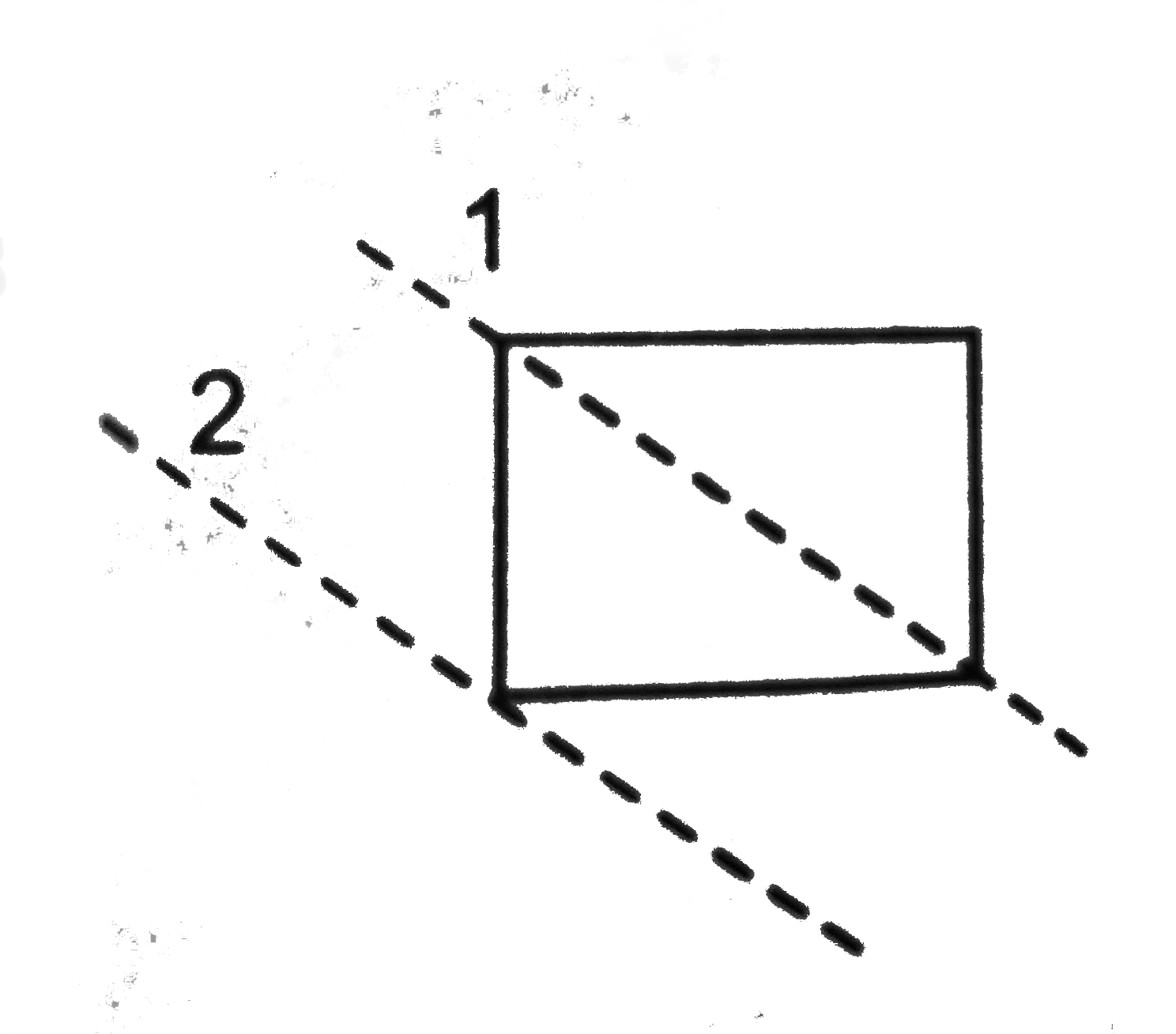
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 is
View SolutionLet IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not. Then
View SolutionLet IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
View SolutionA man spinning in free space can change the moment of inertia of his body (I) by changing its shape. In this process,
View SolutionShow that moment of inertia of a solid body of any shape changes with temperature as I=I0(1+2αθ). Where I0 is the moment of inertia at 0∘C and α is the coefficient of linear expansion of the solid.
View SolutionThe moment of inertia of a uniform rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. Then I1/I2 is
View SolutionIf I1,I2 and I3 are the moments of inertia about the natural axies of solid sphere, hollow sphere and a spherical shell of same mass and radii, the correct result of the following is
View Solution
