Evaluate : (i53+1i53)
To evaluate the expression i53+1i53, we can follow these steps:
Step 1: Simplify i53
We know that the powers of i (the imaginary unit) cycle every 4:
- i1=i
- i2=−1
- i3=−i
- i4=1
To find i53, we can reduce the exponent modulo 4:
53mod4=1
This means:
i53=i1=i
Step 2: Calculate 1i53
Since we found that i53=i, we can now find 1i53:
1i53=1i
To simplify 1i, we can multiply the numerator and the denominator by i:
1i=ii2=i−1=−i
Step 3: Combine the results
Now we can substitute back into the original expression:
i53+1i53=i+(−i)=0
Final Answer
Thus, the value of i53+1i53 is:
0
We know that the powers of i (the imaginary unit) cycle every 4:
- i1=i
- i2=−1
- i3=−i
- i4=1
53mod4=1
This means:
i53=i1=i
Since we found that i53=i, we can now find 1i53:
1i53=1i
To simplify 1i, we can multiply the numerator and the denominator by i:
1i=ii2=i−1=−i
Now we can substitute back into the original expression:
i53+1i53=i+(−i)=0
Thus, the value of i53+1i53 is:
0
Similar Questions
Evaluate:
−1855÷(−53)
View SolutionEvaluate: 2tan53∘cot37∘−cot80∘tan10∘
View SolutionEvaluate: 2tan53∘cot37∘−cot80∘tan10∘
View SolutionEvaluate the following :
(i)sin58∘cos32∘
(ii) sec42∘cosec48∘
(iii)tan37∘cot53∘
View SolutionCalculate the amount of .53I128(t1/2=25min) left after 75 minutes.
View SolutionExpress each of the following fractions as a percent:
(i)34
(ii) 53100
View SolutionEnthalpy change of a reaction with be equal to
View SolutionFind the value of x if
∣∣ ∣∣21x+1−13−40−53∣∣ ∣∣=0
View SolutionThe V−I graphs of parallel and series combinations of two metallic resistors are shown in (Fig. 3.53). Which graph represents the parallel combinations ?
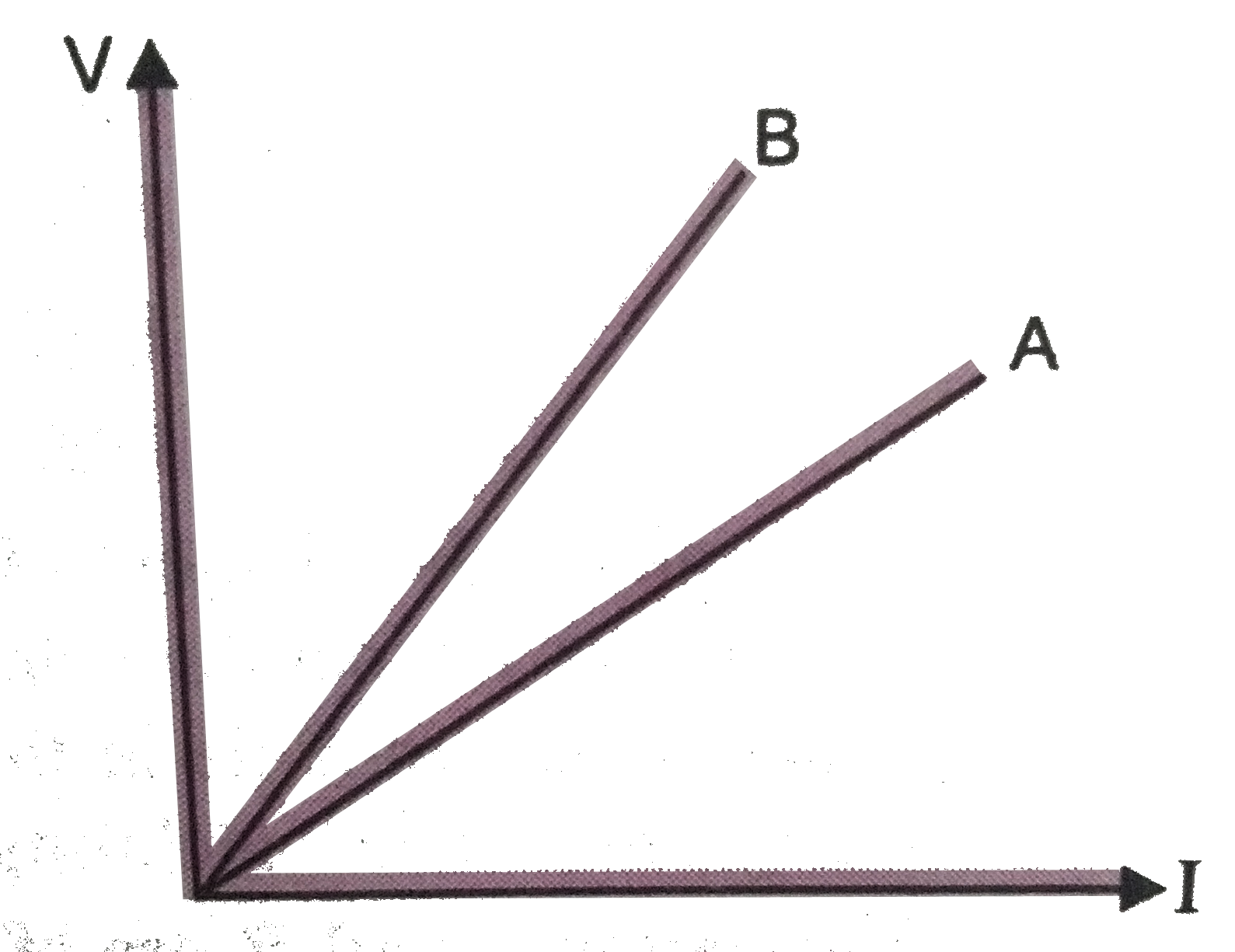 .
.
View SolutionConvert the followng into products:
(i) sin53∘+sin21∘,(ii)cos83∘−cos17∘,(iii)sin50∘−cos80∘
View Solution
