A man runs along a straight road. Naturally he leans a little in the forward direction. The angle with the horizontal line and the line joining the man's centre of mass with the point of support is α ( assume mass per unit length of the man is uniform ) . The man will not slip if the coefficient of friction μ satisfies the conditon.
μ>cotα
μ<cotα
μ>tanα
μ<tanα
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the man as he runs along the road and the condition for him not to slip.
1. Identify Forces Acting on the Man:
- The weight of the man (mg) acts downwards at his center of mass.
- The normal reaction force (N) acts vertically upwards from the ground.
- The frictional force (f) acts horizontally in the direction opposite to the potential slipping.
2. Establish the Geometry:
- The man leans forward at an angle α with respect to the horizontal.
- The line joining the man's center of mass to the point of support (ground) forms this angle α.
3. Set Up Torque Equation:
- To prevent slipping, the net torque about the center of mass must be zero.
- The torque due to friction (f) and the torque due to the normal force (N) must balance each other.
- The distance from the center of mass to the point of action for friction is L2sinα and for the normal force is L2cosα.
4. Write the Torque Balance Equation:
- The equation can be expressed as:
f⋅(L2sinα)−N⋅(L2cosα)=0
- Simplifying this gives:
fsinα=Ncosα
5. Express Friction in Terms of Normal Force:
- From the balance of forces, we know that the normal force N is equal to the weight of the man mg:
N=mg
- Substituting this into the torque equation gives:
fsinα=mgcosα
- Rearranging, we find:
f=mgcotα
6. Condition for No Slipping:
- The maximum static friction force is given by:
fmax=μN=μmg
- For the man not to slip, the frictional force must be less than or equal to the maximum static friction:
mgcotα≤μmg
- Dividing through by mg (assuming mg≠0):
cotα≤μ
7. Final Condition:
- Thus, the condition for the man not to slip while running is:
cotα<μ
Conclusion:
The man will not slip if the coefficient of friction μ satisfies the condition cotα<μ.
- The weight of the man (mg) acts downwards at his center of mass.
- The normal reaction force (N) acts vertically upwards from the ground.
- The frictional force (f) acts horizontally in the direction opposite to the potential slipping.
- The man leans forward at an angle α with respect to the horizontal.
- The line joining the man's center of mass to the point of support (ground) forms this angle α.
- To prevent slipping, the net torque about the center of mass must be zero.
- The torque due to friction (f) and the torque due to the normal force (N) must balance each other.
- The distance from the center of mass to the point of action for friction is L2sinα and for the normal force is L2cosα.
- The equation can be expressed as:
f⋅(L2sinα)−N⋅(L2cosα)=0
- Simplifying this gives:
fsinα=Ncosα
- From the balance of forces, we know that the normal force N is equal to the weight of the man mg:
N=mg
- Substituting this into the torque equation gives:
fsinα=mgcosα
- Rearranging, we find:
f=mgcotα
- The maximum static friction force is given by:
fmax=μN=μmg
- For the man not to slip, the frictional force must be less than or equal to the maximum static friction:
mgcotα≤μmg
- Dividing through by mg (assuming mg≠0):
cotα≤μ
- Thus, the condition for the man not to slip while running is:
cotα<μ
The man will not slip if the coefficient of friction μ satisfies the condition cotα<μ.
Similar Questions
A man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
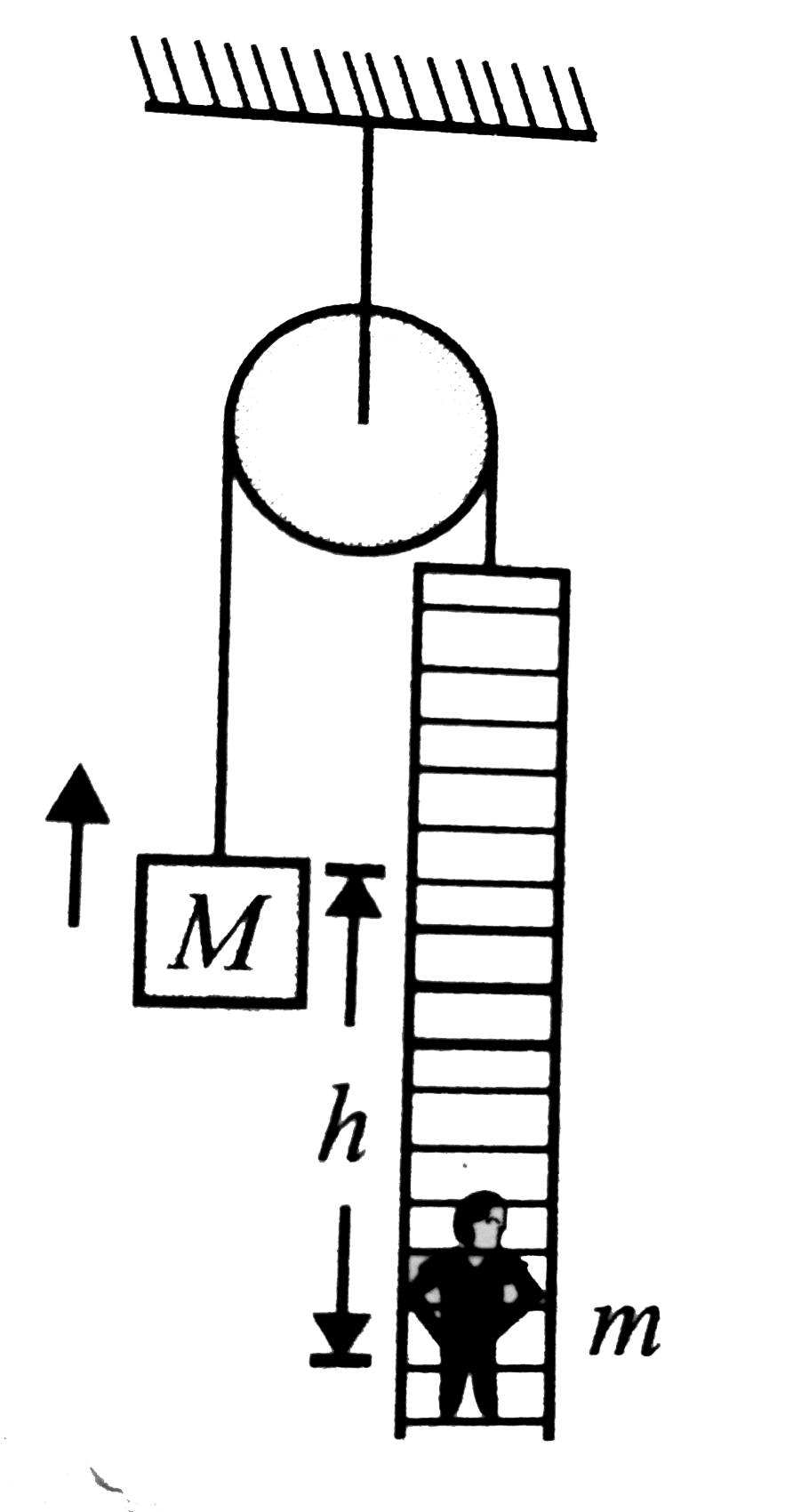
View SolutionA stationary light, smooth pulley can rotate without friction about a fixed horizontal axis. A light rope passes over the pulley. One end of the rope supports a ladder with man and the other end supports a counterweight of mass M. Mass of the man is m. initially, the centre of mass of the counterweight is at a height h from that of man as shown in Fig.
If the man starts to climb up the ladder slowly, calculate work done by him to reach his centre of mass in level with that of the counterweight.
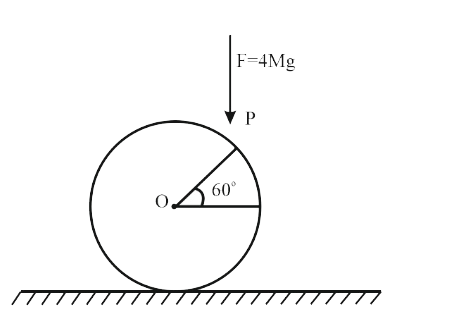
View SolutionA uniform solid sphere of mass M and radius R is lying on a rough horizonal plane. A constant force F=4Mg acts vertically downwards at point P such that the line OP makes an angle of 60∘ with the horizontal as shown in the figure. The minimum value of the coefficient of friction μ so that sphere performs pure rolling, is
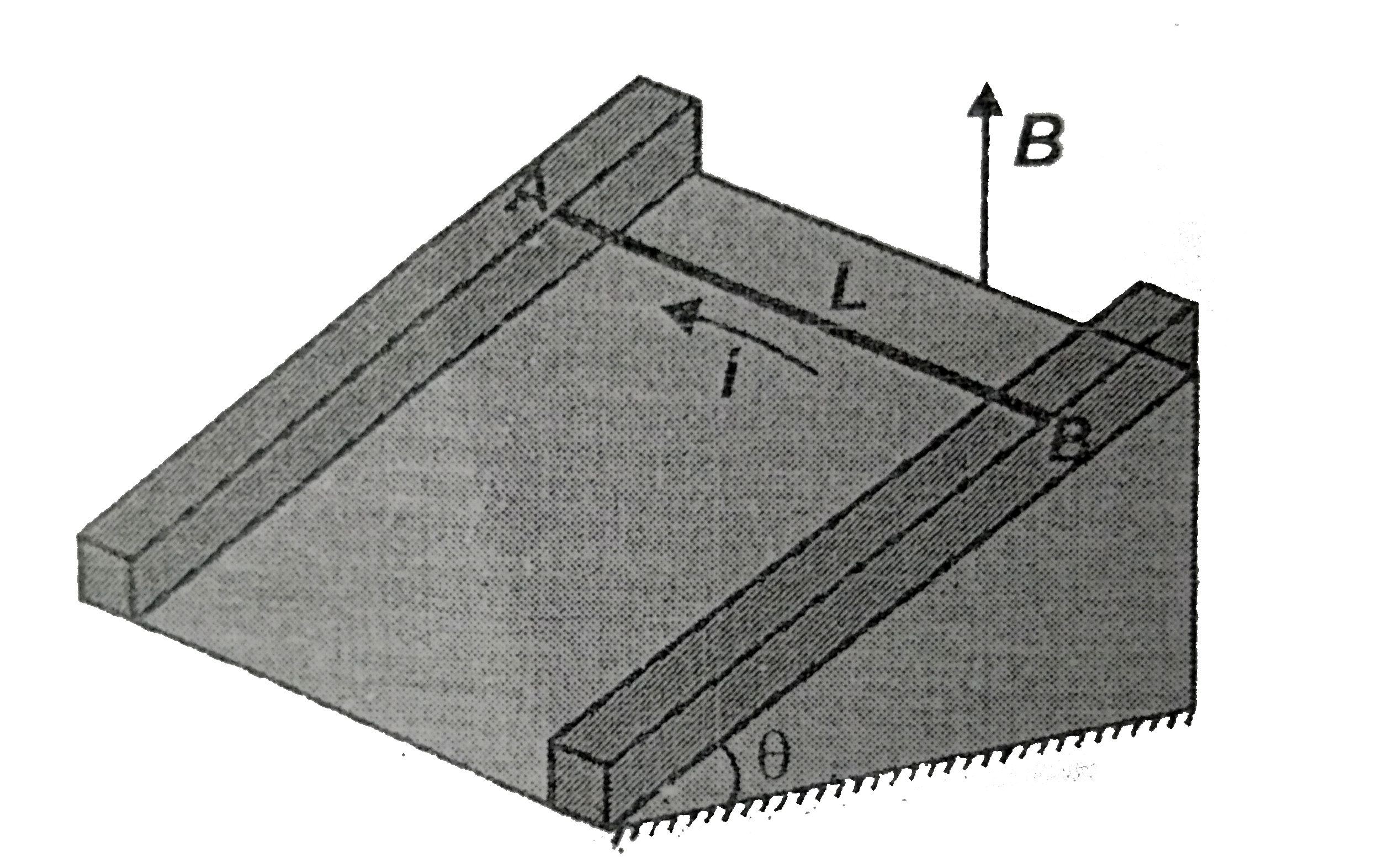
View SolutionOn an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
View Solutiona. A rail road flat car of mass M can roll without friction along a straight horizontal track . Initially, a man of mass m is standing on the car which is moving to the right with speed v0. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is vrel just before he jumps off at the left end?
b. If there are n men each of mass m on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?

View SolutionA plank of mass M is placed on a rough horizontal surface. A man m walks on the plank with an acceleration 'a' while the plank is also acted upon by a horizontal force F whose magnitude and direction can be adjusted to keep the plank at rest.
The coefficient of friction between plank and surface is μ. Choose the correct options.
 .
.
View SolutionA uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

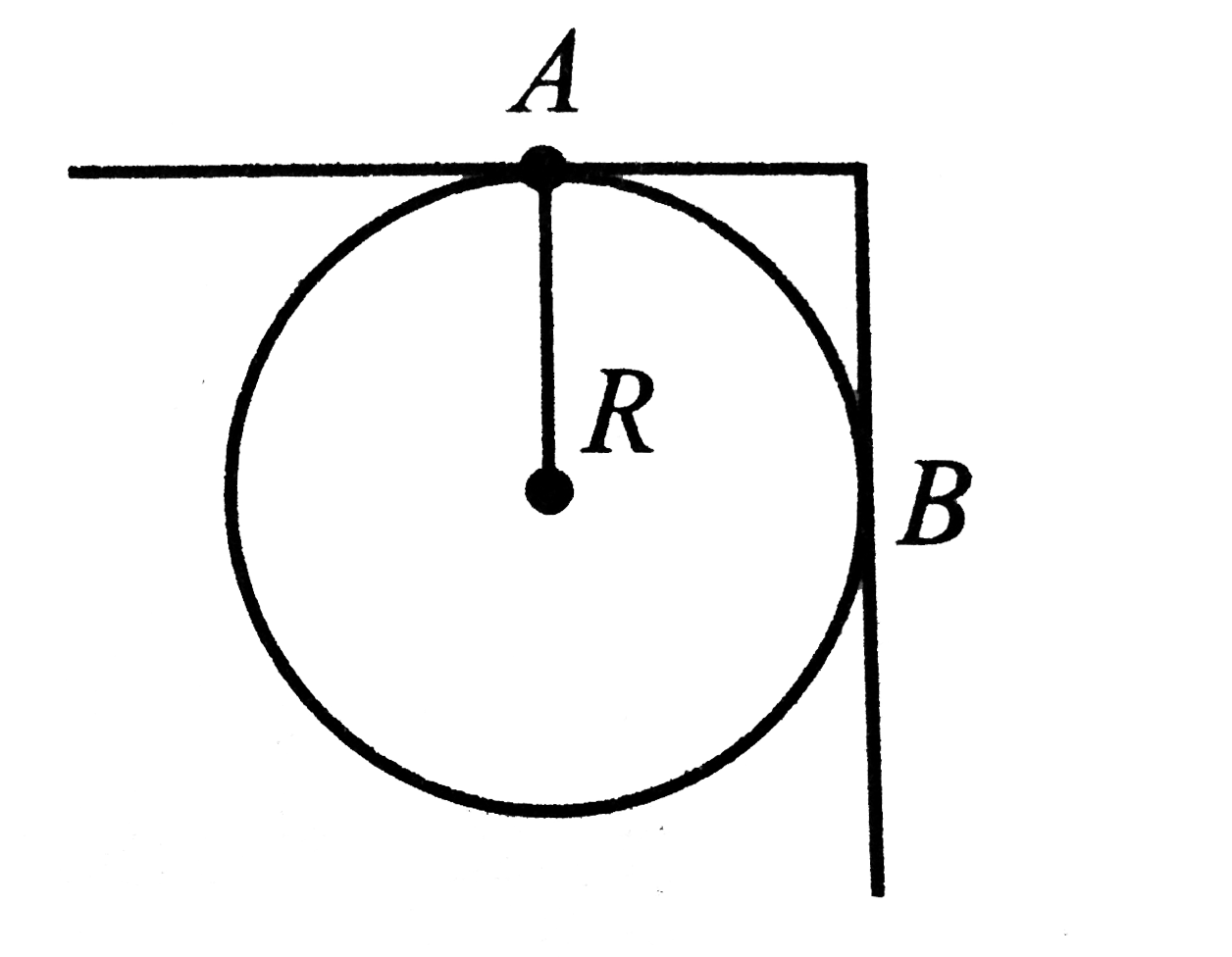
View SolutionA rod bent at right angle along its centre line is placed on a rough horizontal fixed cylinder of radius R as shown in the figure. Mass of the rod is 2m and the rod is in equilibrimu. Assume that the friction force on rod at A and B is equal in magnitude.
View Solution
Two identical discs of mass m and of radius R touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal smooth tabletop. There is a third disc of mass M and of radius R at rest, at a point on thhe perpendicular bisector of of the line segment joining the centres of mass of the two moving discs as shown in the figure. The two moving discs collide elastically with the third one, which is at rest there is no friction between the rims of the discs. What should the ratio of M/m be in order that after the collision the two discs of mass m move perpendicularly to their intial velocity?
View Solution