Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose tha Emech= 8 J, the incorrect statement for this system is :
![Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose tha E(]()
x4, K.E. is constant throughout the region. B. at x < x1 K.E. is smallest and the particle is moving at the slowest speed. C. at x = x2 , K.E is greatest and the particle is moving at the fastest speed. D. at x = x3, K.E. = 4 J" loading="eager" src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/JM_21_S2_20210727_PHY_07_Q01.png" width="80%" class="mx-auto" style="background:white;">
A. at x > x4, K.E. is constant throughout the region.
B. at x < x1 K.E. is smallest and the particle is moving at the slowest speed.
C. at x = x2 , K.E is greatest and the particle is moving at the fastest speed.
D. at x = x3, K.E. = 4 J
at x > x4, K.E. is constant throughout the region.
at x < x1 K.E. is smallest and the particle is moving at the slowest speed.
at x = x2 , K.E is greatest and the particle is moving at the fastest speed.
at x = x3, K.E. = 4 J
The correct Answer is:A
Step by step video & image solution for Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose tha E_("mech")= 8 J, the incorrect statement for this system is : <BR><BR>A. at x > x_4, K.E. is constant throughout the region.<BR>B. at x < x_1 K.E. is smallest and the particle is moving at the slowest speed.<BR>C. at x = x_2 , K.E is greatest and the particle is moving at the fastest speed.<BR>D. at x = x_3, K.E. = 4 J by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
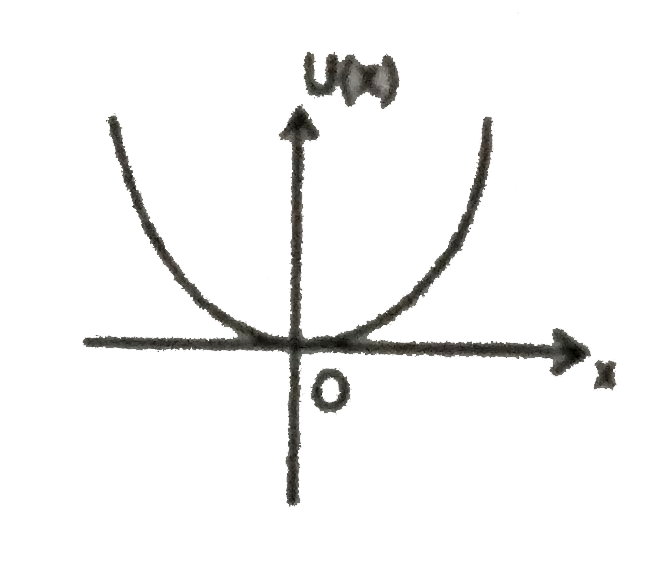
Figure shows a plot of potential energy function U(x)=kx2 where x=displacement and k=constant. Identify the correct conservative force function F(x)
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionA potential energy function for a two-dimensional force is the form U=3x2y−7x. Find the force that acts at the point (x,y).
View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View SolutionThe potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
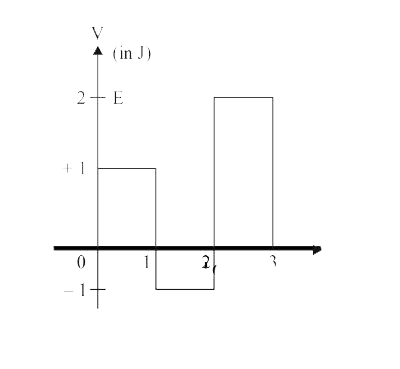
View SolutionThe potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionA particle free to move along the x−axis has potential energy given by U(x)=k[1−e−x2] for −∞≤x≤+∞, where k is a positive constant of appropriate dimensions. Then select the incorrect option
View SolutionA conservative force acts on a 4 kg particle in x direction. The potential energy U(x) is given by U(X)=40+(x–6)2, where x is in metre. If it is given that at x = 8 m, KE is 30 J then find the maximum KE of the particle.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View Solution