A cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
E
E/2
E/4
3/2
The correct Answer is:B
To solve the problem of finding the potential difference between the terminals of a cell with an electromotive force (e.m.f.) E and internal resistance r connected across an external resistance R, we can follow these steps:
1. Identify the Circuit Components:
- We have a cell with e.m.f. E and internal resistance r.
- The cell is connected to an external resistance R.
2. Determine the Total Resistance:
- The total resistance in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=R+r
3. Apply Ohm's Law to Find Current:
- According to Ohm's Law, the current I flowing through the circuit can be calculated as:
I=ERtotal=ER+r
4. Calculate the Potential Difference Across the Cell:
- The potential difference VAB between the terminals of the cell can be expressed as:
VAB=E−I⋅r
- Substituting the expression for I:
VAB=E−(ER+r)⋅r
5. Simplify the Expression:
- Now, simplifying the equation:
VAB=E−E⋅rR+r
- This can be rewritten as:
VAB=E(1−rR+r)
- Further simplifying gives:
VAB=E(RR+r)
6. Final Result:
- The potential difference between the terminals of the cell is:
VAB=E⋅RR+r
- We have a cell with e.m.f. E and internal resistance r.
- The cell is connected to an external resistance R.
- The total resistance in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=R+r
- According to Ohm's Law, the current I flowing through the circuit can be calculated as:
I=ERtotal=ER+r
- The potential difference VAB between the terminals of the cell can be expressed as:
VAB=E−I⋅r
- Substituting the expression for I:
VAB=E−(ER+r)⋅r
- Now, simplifying the equation:
VAB=E−E⋅rR+r
- This can be rewritten as:
VAB=E(1−rR+r)
- Further simplifying gives:
VAB=E(RR+r)
- The potential difference between the terminals of the cell is:
VAB=E⋅RR+r
Similar Questions
A cell of emf E is connected across a resistance R. The potential difference between the terminals of the cell is found to be V. The internal resistance of the cell must be -
View SolutionA resistance R is connected across a cell of emf ε and internal resistance r. A potentiometer now measures the potential difference between the terminals of the cell is V. Write the expression for r in terms of ε, V and R.
View SolutionFor the determination of emf E and internal resistance 'r' of a cell , the graph is obtained between potential difference V between the terminal of the cell against the current l, which was changed by adjusting the rheostat, is as shown . The internal resistance of the cell is
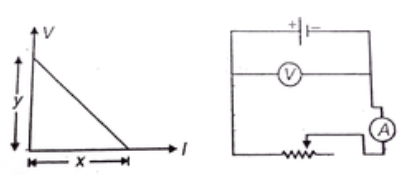
View SolutionThe emf of a cell is ε and its internal resistance is r. its terminals are connected to a resistance R. The potential difference between the terminals is 1.6V for R=4Ω, and 1.8V for R=9Ω. Then,
View SolutionThe emf of a cell is ε and its internal resistance is r. its termnals are cannected to a resistance R. The potential difference between the terminals is 1.6V for R = 4 Omega, and 1.8 V for R = 9 Omega. Then,
View SolutionA cell of e.m.f E and internal resitance r ,is connected to an external resistance R. the variation of potential difference V across the resistance R as function of R as shown in the figure, is the best represented by curve
_PHY_E01_011_Q01.png)
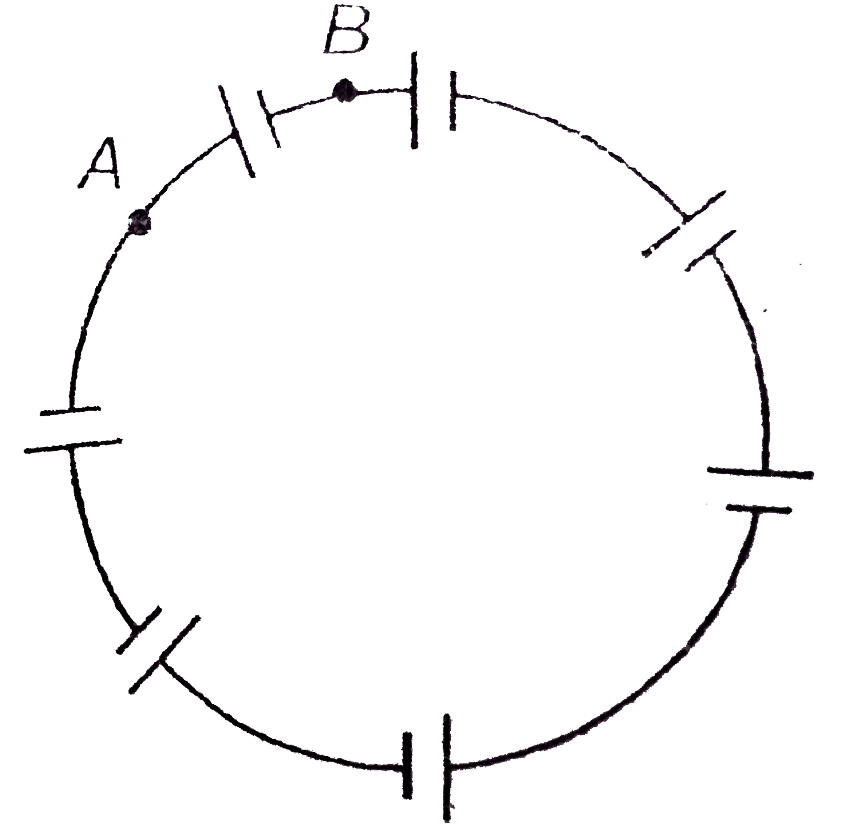
View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of e.m.f. 'E' and internal resistance 'r' is connected across a variable resistor 'R'. Plot a graph showing the variation of terminal potential 'V' with resistance R.
Predict from the graph the condition under which 'V' becomes equal of 'E'

View Solution
