A circuit consists of a resistance R connected to n similar cells. If the current in the circuit is the same whether the cells are connected in series or in parallel, then the internal resistancer of each cell is given by
r=R/n
r=nR
r=R
r=1/R
The correct Answer is:C
To solve the problem, we need to analyze the circuit with n similar cells connected in both series and parallel configurations, and then derive the expression for the internal resistance of each cell.
1. Understanding the Circuit Configuration:
- We have n similar cells, each with an EMF (E) and an internal resistance (r).
- The external resistance in the circuit is denoted as R.
2. Cells Connected in Series:
- When the cells are connected in series, the total EMF (E_eq) is:
Eeq=nE
- The total internal resistance (r_eq) is:
req=nr
- The total resistance in the circuit when cells are in series is:
Rtotal=R+nr
- Using Ohm's law, the current (I) in the circuit can be expressed as:
I=EeqRtotal=nER+nr
3. Cells Connected in Parallel:
- When the cells are connected in parallel, the total EMF (E_eq) remains the same:
Eeq=E
- The total internal resistance (r_eq) for n cells in parallel is:
req=rn
- The total resistance in the circuit when cells are in parallel is:
Rtotal=R+rn
- The current (I') in the circuit can be expressed as:
I′=EeqRtotal=ER+rn
4. Setting the Currents Equal:
- According to the problem, the current is the same in both configurations:
I=I′
- Therefore, we can set the two expressions for current equal to each other:
nER+nr=ER+rn
5. Cross-Multiplying and Simplifying:
- Cross-multiplying gives us:
nE(R+rn)=E(R+nr)
- Simplifying this, we get:
nR+r=R+nr
- Rearranging terms leads to:
nR−R=nr−r
- Factoring out common terms gives us:
(n−1)R=(n−1)r
6. Finding Internal Resistance:
- Assuming n≠1 (since if n=1, there is no difference between series and parallel), we can divide both sides by (n - 1):
R=r
- Thus, the internal resistance of each cell is equal to the external resistance.
Final Answer:
The internal resistance of each cell is given by:
r=R
- We have n similar cells, each with an EMF (E) and an internal resistance (r).
- The external resistance in the circuit is denoted as R.
- When the cells are connected in series, the total EMF (E_eq) is:
Eeq=nE
- The total internal resistance (r_eq) is:
req=nr
- The total resistance in the circuit when cells are in series is:
Rtotal=R+nr
- Using Ohm's law, the current (I) in the circuit can be expressed as:
I=EeqRtotal=nER+nr
- When the cells are connected in parallel, the total EMF (E_eq) remains the same:
Eeq=E
- The total internal resistance (r_eq) for n cells in parallel is:
req=rn
- The total resistance in the circuit when cells are in parallel is:
Rtotal=R+rn
- The current (I') in the circuit can be expressed as:
I′=EeqRtotal=ER+rn
- According to the problem, the current is the same in both configurations:
I=I′
- Therefore, we can set the two expressions for current equal to each other:
nER+nr=ER+rn
- Cross-multiplying gives us:
nE(R+rn)=E(R+nr)
- Simplifying this, we get:
nR+r=R+nr
- Rearranging terms leads to:
nR−R=nr−r
- Factoring out common terms gives us:
(n−1)R=(n−1)r
- Assuming n≠1 (since if n=1, there is no difference between series and parallel), we can divide both sides by (n - 1):
R=r
- Thus, the internal resistance of each cell is equal to the external resistance.
The internal resistance of each cell is given by:
r=R
Similar Questions
Under what condition will the current in a wire be the same when connected in series and in parallel on n identical cells each having internal resistance r and external resistance R?
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
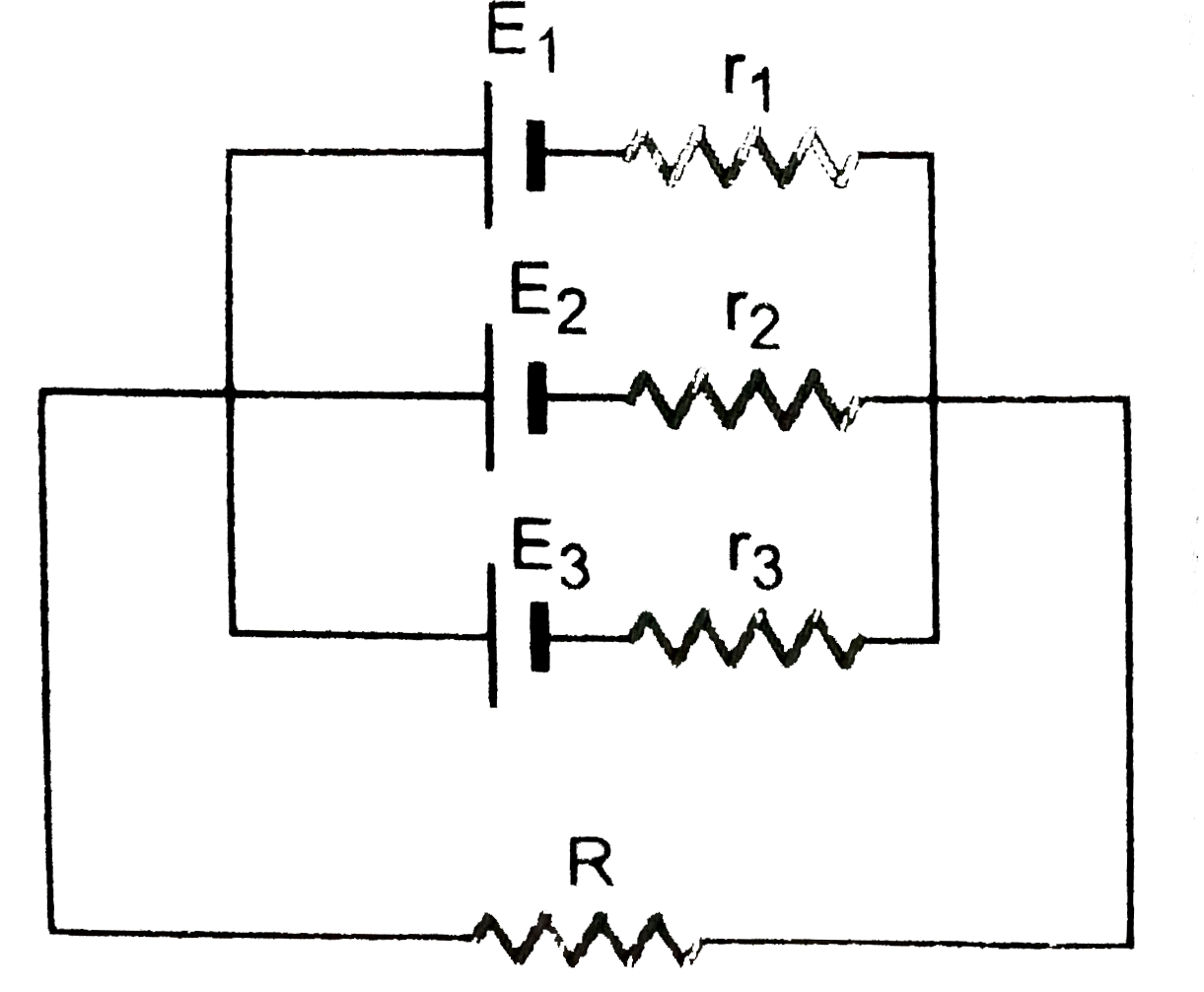
View Solution
Knowledge Check
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
If internal resistance of cell is negligible, then current flowing through the circuit is
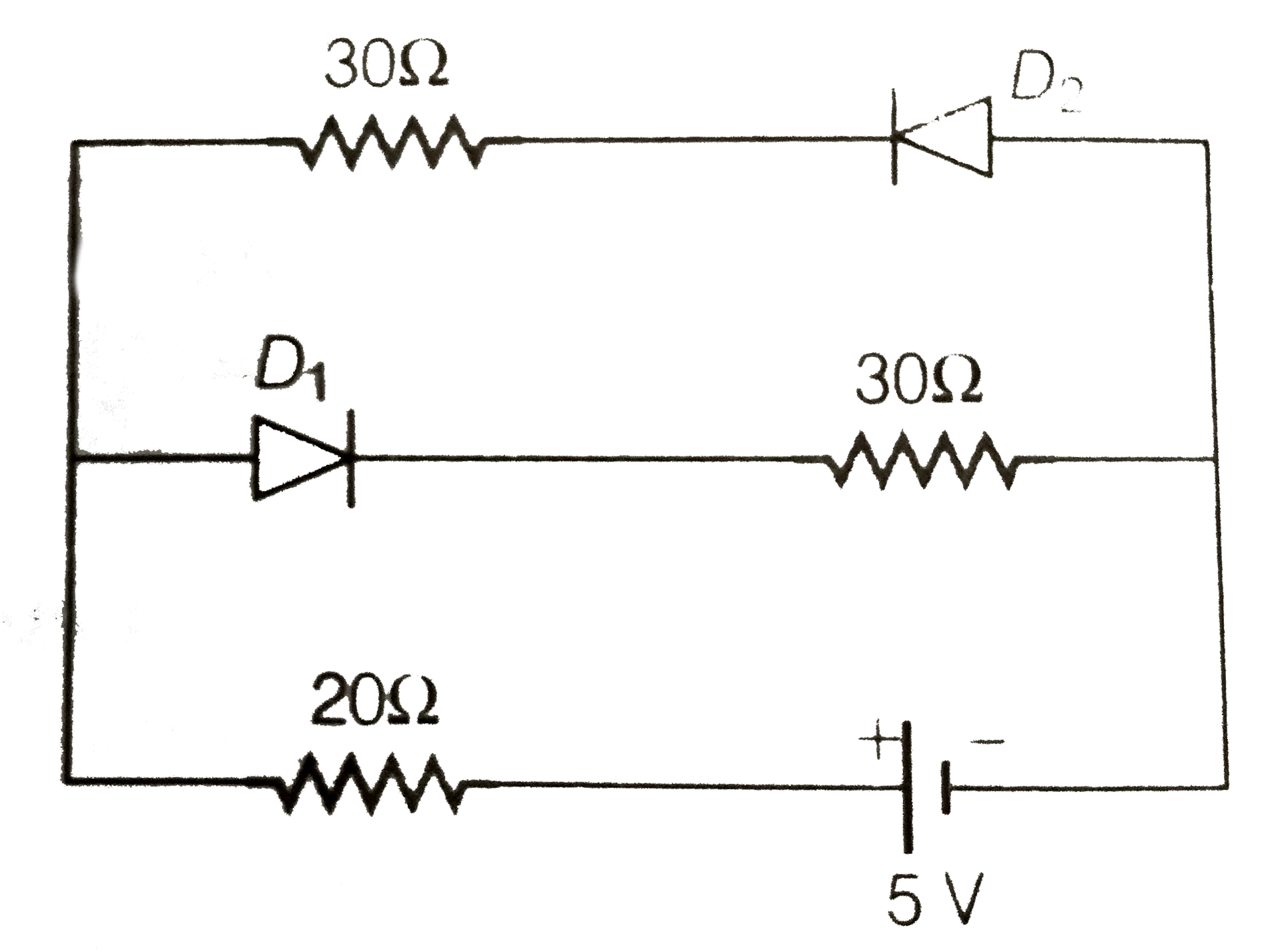
View SolutionFor the given circuit,
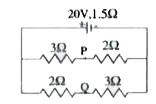
If internal resistance of cell is 1.5Ω, then
View Solutionn equal cell having emf E and internal resistance r, are connected in circuit of a resistance R. Same current flows in circuit either they connected in series or parallel, if:
View Solutioncells can be connected in series ,in parallel and as well as combination of both the series and parallel .
View SolutionTwo identical cells of emf 1.5 V each joined in paralllel provide supply to an external circuit consisting of two resistances of 7Ω each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.
View SolutionN identical cells whether joined together in series or in parallel, give the same current, when connected to an external resistance of 'R'. The internal resistance of each cell is:-
View SolutionWhen 10 identical cells in sereis are connected to the ends of a resistance of 59Ω, the current is found to be 0.25A. But when the nsame cells, being connected in parallel, are joined to the ends of a resistance of 0.05Omega, the current is 25A. Calculate the internal resistance and the emf of each cell.

View Solution
