Two identical cells of emf 1.5 V each joined in paralllel provide supply to an external circuit consisting of two resistances of 7Ω each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.
To calculate the internal resistance of each cell in the given circuit, we will follow these steps:
Step 1: Understand the Circuit Configuration
We have two identical cells, each with an EMF (E) of 1.5 V, connected in parallel. The external circuit consists of two resistors (R1 and R2), each of 7 Ω, also connected in parallel.
Step 2: Calculate the Equivalent Resistance of the External Circuit
The equivalent resistance (R_ext) of two resistors in parallel can be calculated using the formula:
Rext=R1⋅R2R1+R2
Substituting the values:
Rext=7⋅77+7=4914=3.5Ω
Step 3: Calculate the Total EMF and Internal Resistance
Since the cells are in parallel, the equivalent EMF (E_eq) remains the same as the individual cells:
Eeq=1.5V
Let the internal resistance of each cell be r. When the cells are in parallel, the total internal resistance (R_int) can be calculated as:
Rint=r2
Step 4: Use the Terminal Voltage to Find the Current
The terminal voltage (V_t) is given as 1.4 V. According to Ohm's law, the current (I) flowing through the circuit can be calculated using the total voltage and total resistance:
Vt=Eeq−I⋅Rint
Substituting the known values:
1.4=1.5−I⋅r2
Rearranging gives:
I⋅r2=1.5−1.4=0.1(1)
Step 5: Calculate the Total Current in the Circuit
The total resistance in the circuit is the sum of the equivalent internal resistance and the external resistance:
Rtotal=Rint+Rext=r2+3.5
Using Ohm's law again, we can express the current (I):
I=EeqRtotal=1.5r2+3.5(2)
Step 6: Substitute Equation (2) into Equation (1)
Substituting the expression for I from (2) into (1):
(1.5r2+3.5)⋅r2=0.1
Cross-multiplying gives:
1.5r=0.1(r2+3.5)
Expanding and simplifying:
1.5r=0.05r+0.35
1.5r−0.05r=0.35
1.45r=0.35
r=0.351.45≈0.2414Ω
Final Answer
The internal resistance of each cell is approximately:
r≈0.2414Ω
We have two identical cells, each with an EMF (E) of 1.5 V, connected in parallel. The external circuit consists of two resistors (R1 and R2), each of 7 Ω, also connected in parallel.
The equivalent resistance (R_ext) of two resistors in parallel can be calculated using the formula:
Rext=R1⋅R2R1+R2
Substituting the values:
Rext=7⋅77+7=4914=3.5Ω
Since the cells are in parallel, the equivalent EMF (E_eq) remains the same as the individual cells:
Eeq=1.5V
Rint=r2
The terminal voltage (V_t) is given as 1.4 V. According to Ohm's law, the current (I) flowing through the circuit can be calculated using the total voltage and total resistance:
Vt=Eeq−I⋅Rint
Substituting the known values:
1.4=1.5−I⋅r2
Rearranging gives:
I⋅r2=1.5−1.4=0.1(1)
The total resistance in the circuit is the sum of the equivalent internal resistance and the external resistance:
Rtotal=Rint+Rext=r2+3.5
Using Ohm's law again, we can express the current (I):
I=EeqRtotal=1.5r2+3.5(2)
Substituting the expression for I from (2) into (1):
(1.5r2+3.5)⋅r2=0.1
Cross-multiplying gives:
1.5r=0.1(r2+3.5)
Expanding and simplifying:
1.5r=0.05r+0.35
1.5r−0.05r=0.35
1.45r=0.35
r=0.351.45≈0.2414Ω
The internal resistance of each cell is approximately:
r≈0.2414Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Four identical cells each of emf 2V, are joined in parallel providing supply of current to external circuit consisting of two 15Ω resistors joined in parallel. The terminal voltage of the cells ae read by an ideal voltmeter is 1.6V. Calculate the internal resistance of each cell.
View SolutionA cell supplies a current of 1.2 A through two resistors each of 2 Ω connected in parallel. When the resistors are connected in series, it supplies a current of 0.4 A. Calculate :
the internal resistance,
View SolutionA cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
View SolutionA battery of e.m.f 3 V supplies current through a circuit in which the resistance can be changed. A high resistance voltmeter is connected across the battery. When the current is 1.5 A, the voltmeter reads 2.7 V. Find the internal resistance of the battery.
View SolutionIf the reading of the ideal voltmeter shown in the circuit is 2V the internal resistance of the two identical cells is
_2019_CBT5_E01_030_Q01.png)
View SolutionFig. shows two resistors A of 4Ω and B of 6 Ω joined in series to a battery of e.m.f. 12 V and internal resistance 2 Ω . Calculate :
the terminal voltage of the battery,
View SolutionIn the circuit shown in fig. the cell has emf 10V and internal resistance 1Ω
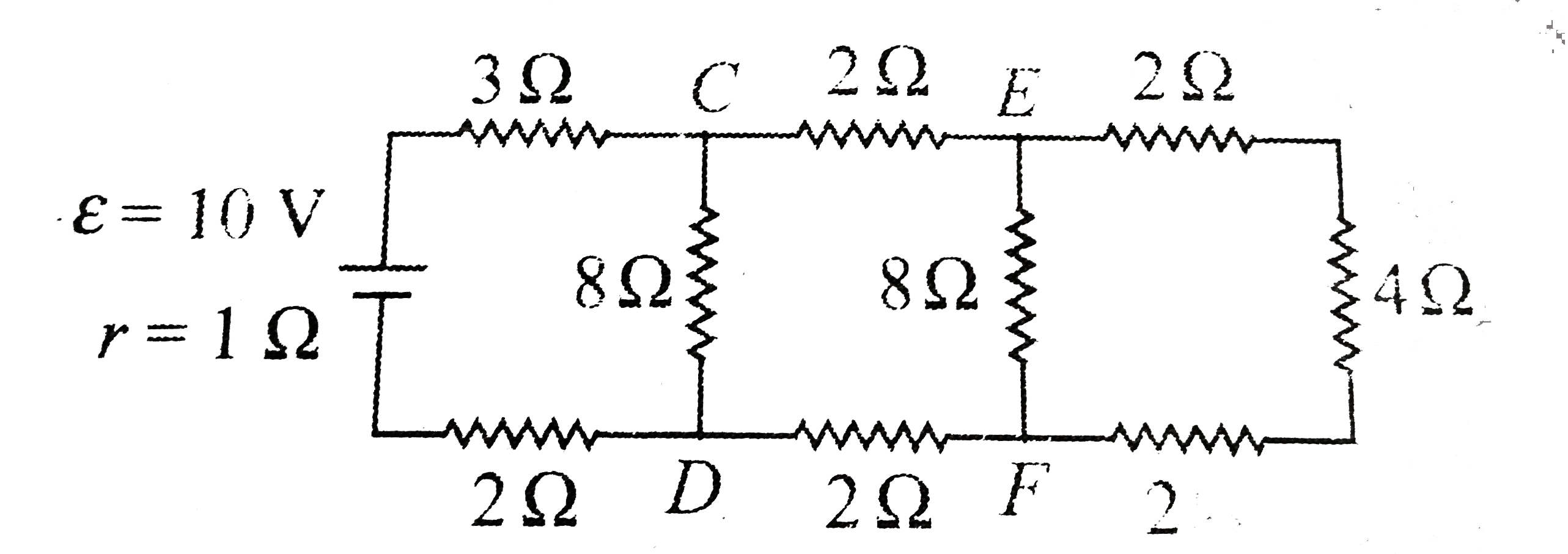
View Solutionn identical cells each of emf 6 V , connected in series with an external resistor of 5Ω, carry a current of 10A. If two cells are connected wrongly in series with the same external resistor, the current flowing through the cells will be 8A. Find the value of n and r the internal resistance of each cell.
View SolutionThe emf of a daniel cell is 1.08V. When the terminals of the cell are connected to resistance of 3Ω, the potential difference across the terminals is found to be 0.6 V. Then , the internal resistance of the cell is
View SolutionN identical cells whether joined together in series or in parallel, give the same current, when connected to an external resistance of 'R'. The internal resistance of each cell is:-
View Solution