Four identical charges are placed at the four vertices of a square lying in YZ plane. A fifth charge is moved along X axis. The variation of potential energy (U) along X axis is correctly represented by
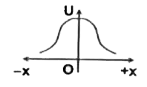


The correct Answer is:B
To solve the problem of determining the variation of potential energy (U) as a fifth charge is moved along the X-axis in the presence of four identical charges located at the vertices of a square in the YZ plane, we can follow these steps:
1. Understanding the Configuration:
- We have four identical charges, each denoted as Q, placed at the vertices of a square in the YZ plane.
- The square has a side length a, and the coordinates of the charges can be represented as:
- (0,a2,a2)
- (0,a2,−a2)
- (0,−a2,a2)
- (0,−a2,−a2)
2. Position of the Fifth Charge:
- The fifth charge, denoted as q, is moved along the X-axis. Its position can be represented as (x,0,0).
3. Calculating the Distance:
- The distance d from the fifth charge to any of the four charges can be calculated using the distance formula. For a charge located at (0,a2,a2), the distance d is:
d=√x2+(a2)2+(a2)2=√x2+a22
4. Potential Energy Calculation:
- The potential energy U due to one charge Q at distance d is given by:
U=kQqd
- Since there are four identical charges, the total potential energy Utotal when the fifth charge is at position x is:
Utotal=4⋅kQqd=4kQq√x2+a22
5. Analyzing the Variation of Potential Energy:
- As x approaches 0, d becomes √a22, which is the minimum distance, leading to maximum potential energy.
- As |x| increases, d increases, leading to a decrease in potential energy.
- Therefore, the potential energy U is symmetric about the origin and reaches a maximum at x=0.
6. Graphical Representation:
- The graph of potential energy U versus x will show a peak at x=0 and will decrease symmetrically as |x| increases.
Conclusion:
The variation of potential energy U along the X-axis is represented by a curve that peaks at the origin and decreases symmetrically as you move away from the origin in either direction.
- We have four identical charges, each denoted as Q, placed at the vertices of a square in the YZ plane.
- The square has a side length a, and the coordinates of the charges can be represented as:
- (0,a2,a2)
- (0,a2,−a2)
- (0,−a2,a2)
- (0,−a2,−a2)
- The fifth charge, denoted as q, is moved along the X-axis. Its position can be represented as (x,0,0).
- The distance d from the fifth charge to any of the four charges can be calculated using the distance formula. For a charge located at (0,a2,a2), the distance d is:
d=√x2+(a2)2+(a2)2=√x2+a22
- The potential energy U due to one charge Q at distance d is given by:
U=kQqd
- Since there are four identical charges, the total potential energy Utotal when the fifth charge is at position x is:
Utotal=4⋅kQqd=4kQq√x2+a22
- As x approaches 0, d becomes √a22, which is the minimum distance, leading to maximum potential energy.
- As |x| increases, d increases, leading to a decrease in potential energy.
- Therefore, the potential energy U is symmetric about the origin and reaches a maximum at x=0.
- The graph of potential energy U versus x will show a peak at x=0 and will decrease symmetrically as |x| increases.
The variation of potential energy U along the X-axis is represented by a curve that peaks at the origin and decreases symmetrically as you move away from the origin in either direction.
Similar Questions
Four equal charges of magnitudes q each are placed at four corners of a square with its centre at origin and lying in y-z plane. Aa fifth charge +Q is moved along x-axis. The electrostatic potential energy (U) varies on x-axis as
View SolutionFour equal charges of magnitudes q each are placed at four corners of a square with its centre at origin and lying in y-z plane. Aa fifth charge +Q is moved along x-axis. The electrostatic potential energy (U) varies on x-axis as
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.

View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionTwo identical positive charges are placed at x=−a and x=a. The correct variation of potential V along the x-axis is given by
View SolutionFour identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View SolutionFour pointed charges are placed on vertices of a square.If all the charges are brought to any one of the vertices.The change in potential at the centre of square due to this would be
View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
View SolutionFour identical point charges are placed at the corners of a square, A fifth point charge placed at the center of the square experiences zero net force . Is this a stable equilirium for the fifth charge? Explain.
View Solution