Two identical positive charges are placed at x=−a and x=a. The correct variation of potential V along the x-axis is given by

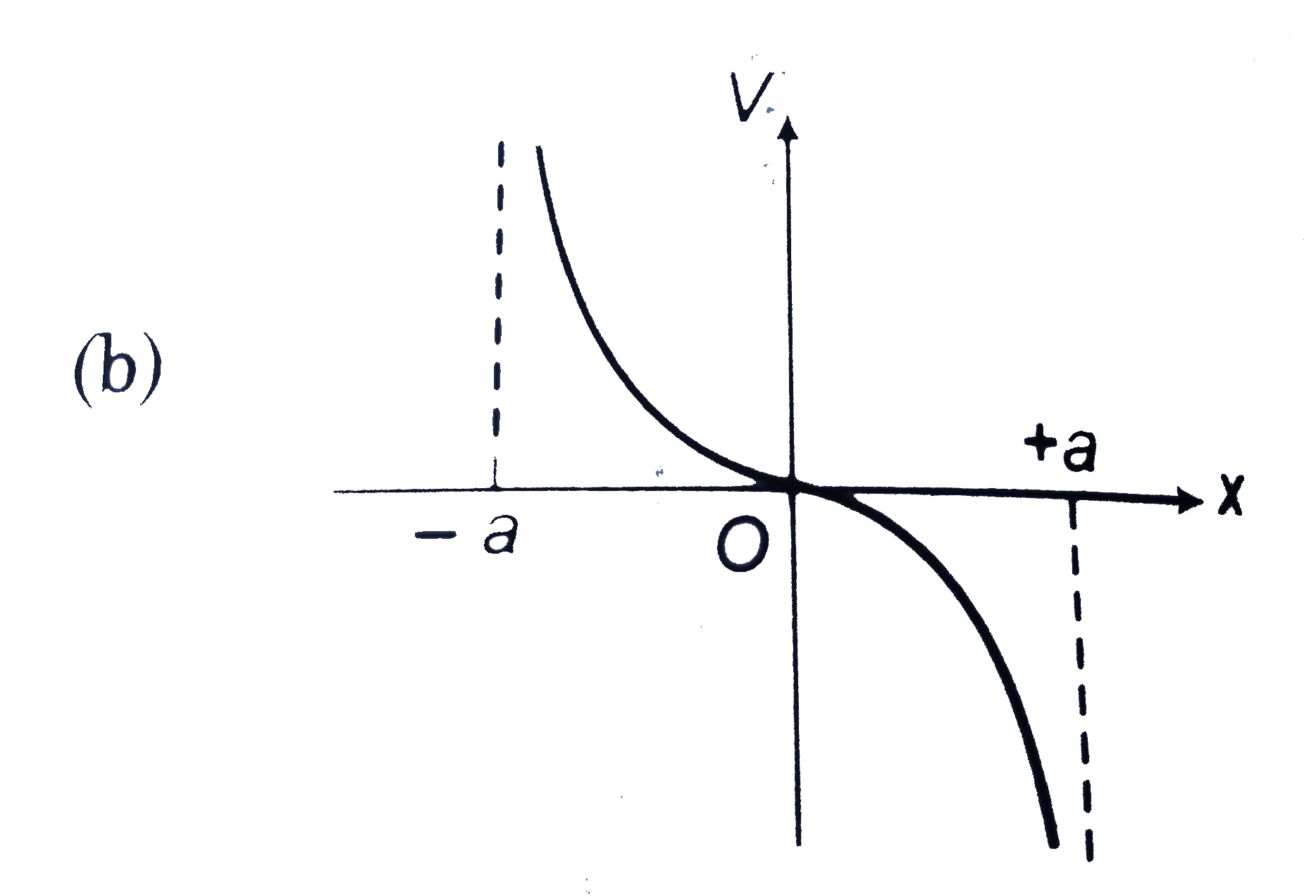

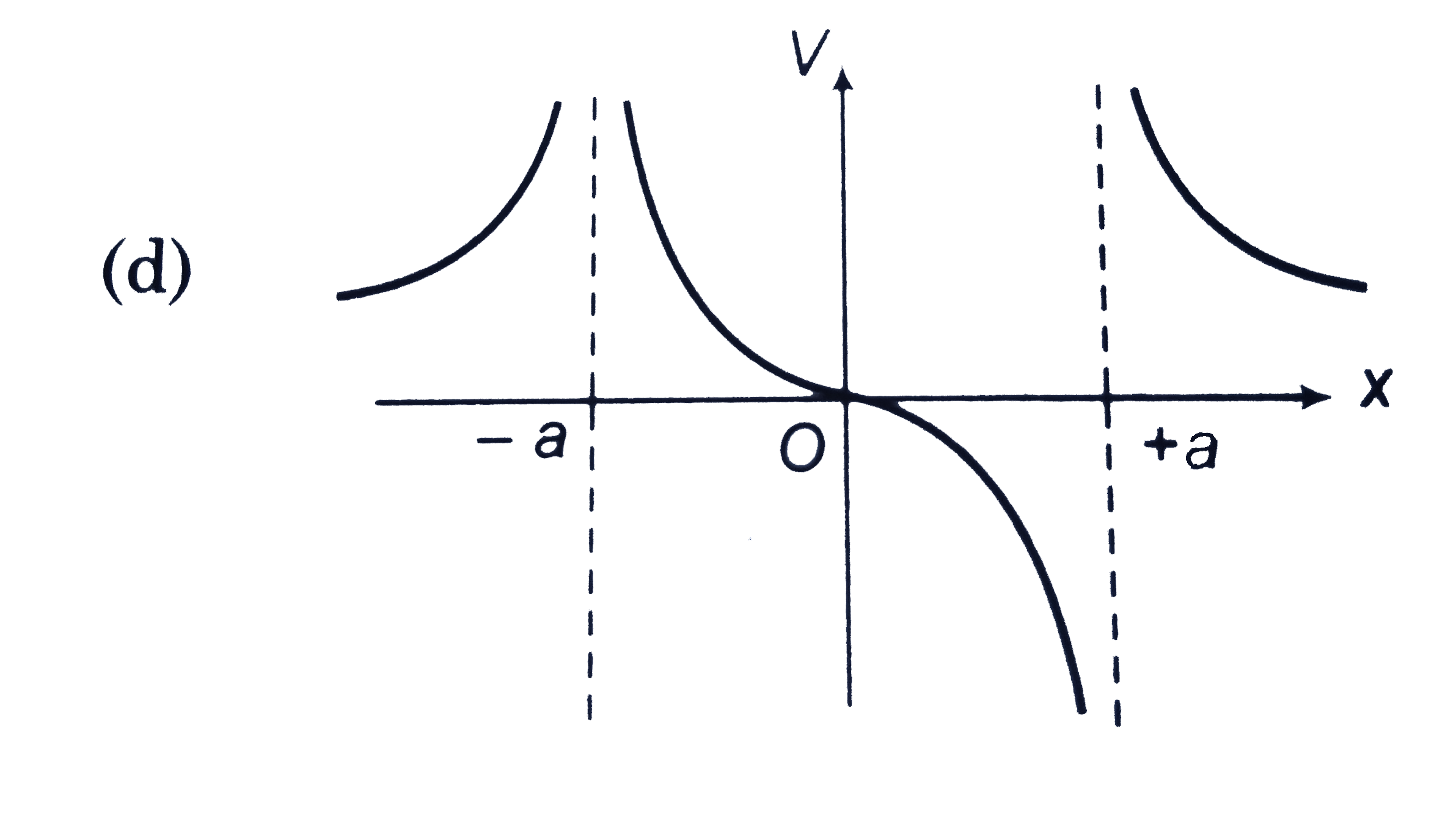
The correct Answer is:C
To solve the problem of finding the variation of electric potential V along the x-axis due to two identical positive charges placed at x=−a and x=a, we can follow these steps:
Step 1: Understand the Configuration
We have two identical positive charges, +Q, located at positions x=−a and x=a. The electric potential V at any point x on the x-axis is the sum of the potentials due to each charge.
Step 2: Write the Expression for Electric Potential
The electric potential V at a point x due to a point charge Q is given by:
V=kQr
where k is Coulomb's constant and r is the distance from the charge to the point where we are calculating the potential.
Step 3: Calculate the Potential at Point x
For our configuration:
- The distance from the charge at x=−a to a point x is |x+a|.
- The distance from the charge at x=a to a point x is |x−a|.
Thus, the total potential V at a point x is:
V(x)=kQ|x+a|+kQ|x−a|
Step 4: Analyze the Potential at Specific Points
1. At the origin x=0:
V(0)=kQ|−a|+kQ|a|=kQa+kQa=2kQa
2. As x approaches −a or a:
- As x approaches −a, |x+a| approaches 0, leading V to approach +∞.
- As x approaches a, |x−a| approaches 0, leading V to approach +∞.
3. As x approaches ±∞:
- As x approaches +∞ or −∞, both |x+a| and |x−a| become very large, thus V approaches 0.
Step 5: Sketch the Graph
- The potential V is +∞ at x=−a and x=a.
- The potential is 2kQa at x=0.
- The potential approaches 0 as x goes to ±∞.
Conclusion
The variation of potential V along the x-axis will have a shape that approaches +∞ at the positions of the charges and approaches 0 as x moves towards ±∞. The correct option representing this variation is option C.
We have two identical positive charges, +Q, located at positions x=−a and x=a. The electric potential V at any point x on the x-axis is the sum of the potentials due to each charge.
The electric potential V at a point x due to a point charge Q is given by:
V=kQr
where k is Coulomb's constant and r is the distance from the charge to the point where we are calculating the potential.
For our configuration:
- The distance from the charge at x=−a to a point x is |x+a|.
- The distance from the charge at x=a to a point x is |x−a|.
V(x)=kQ|x+a|+kQ|x−a|
1. At the origin x=0:
V(0)=kQ|−a|+kQ|a|=kQa+kQa=2kQa
- As x approaches −a, |x+a| approaches 0, leading V to approach +∞.
- As x approaches a, |x−a| approaches 0, leading V to approach +∞.
- As x approaches +∞ or −∞, both |x+a| and |x−a| become very large, thus V approaches 0.
- The potential V is +∞ at x=−a and x=a.
- The potential is 2kQa at x=0.
- The potential approaches 0 as x goes to ±∞.
The variation of potential V along the x-axis will have a shape that approaches +∞ at the positions of the charges and approaches 0 as x moves towards ±∞. The correct option representing this variation is option C.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Two identical point charges are placed at A and B. The potential difference V0−VC is (k=14πε0)
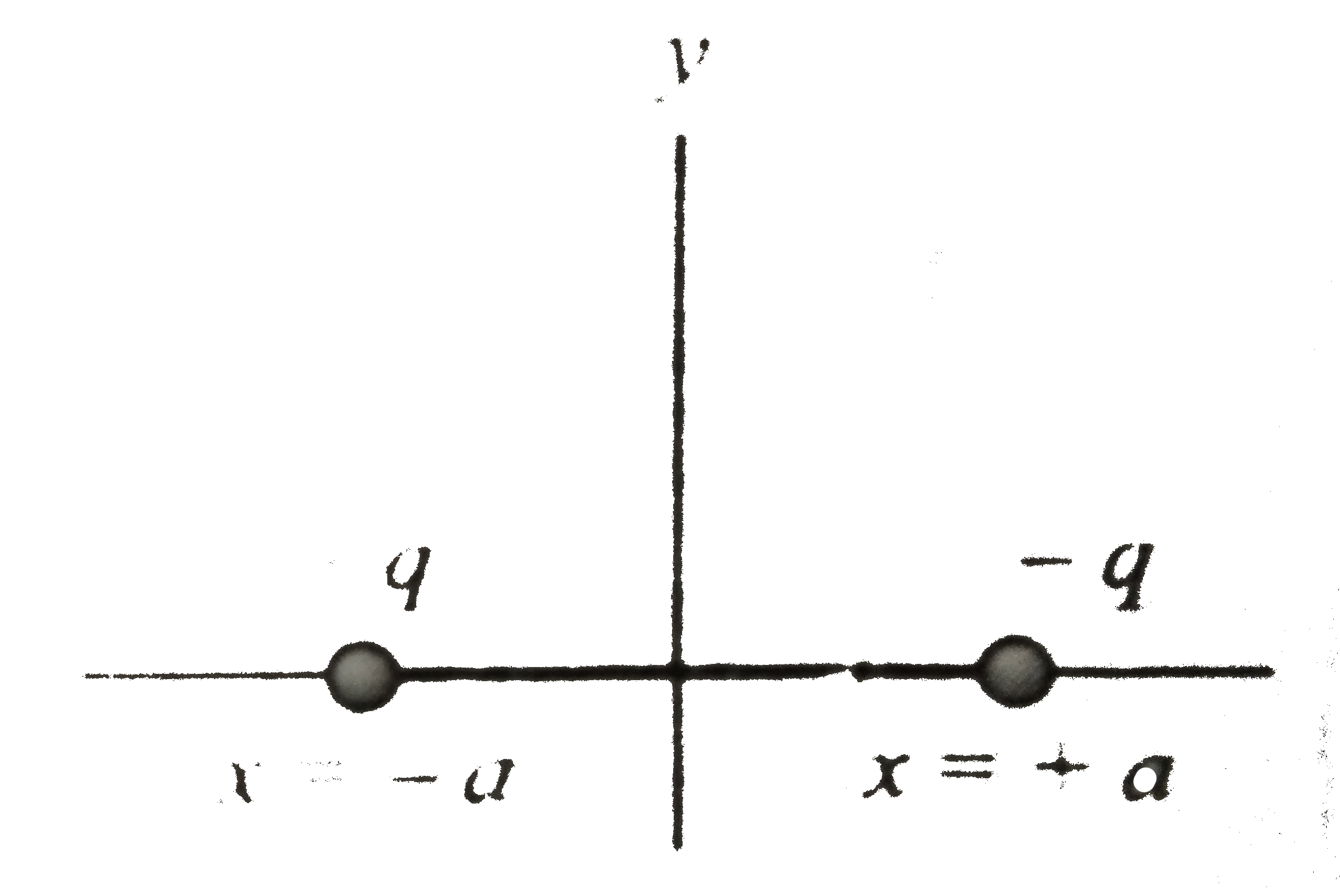
View SolutionTwo point charge ±q are placed on the axis at x=−a and x=+a, as shown in fig.
(i) Plot the variation of E along the x-axis.
(ii) Plot the variation of E along the y-axis.
View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
View SolutionTwo identical positive charges are fixed on the y-axis, at equal distances from the origin O. A particle with a negative charges starts on the x-axis at a large distance from O. moves along the x-axis passes through O, and moves far away from O on the other side. Its acceleration a is taken as positive along its direction of motion. Plot acceleration a of the particle against its x-coordinate.
View SolutionFour identical charges are placed at the four vertices of a square lying in YZ plane. A fifth charge is moved along X axis. The variation of potential energy (U) along X axis is correctly represented by
View SolutionTwo identical infinite positive line changes are places into the lines x=±a in the x=y plane. A positive point charge placed at origin is restricted to move along x-axis its equilibrium is
View SolutionTwo equal point charges are fixed at x=−a and x=+a on the x-axis. Another point charge Q is placed at the origin. The change in the electrical potential energy of Q, when it is displaced by a small distance x along the x-axis, is approximately proportional to
View SolutionThree charges are placed along x- axis at x=−a,x=0 and x=a as shown . Calculate the potential energy of the system.

View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
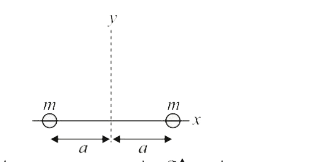
View SolutionTwo identical spherical balls, each of mass m, are placed as shown in figure. Plot the variation of g(gravitation intensity) along the x-axis due to both the masses.
View Solution
