An Infinite current carrying wire having current I0 is placed coaxially inside a hollow conducting infinite cylinder of radius R and having current I flowing along the length of the cylinder in the same direction as I0 what is the increment in magnetic pressure due to placing of the wire?
μ0l0l2π2R2
μ0l0l2πR2
μ0I0I4π2R2
μ0l0l4πR2
The correct Answer is:C
To solve the problem of determining the increment in magnetic pressure due to the placement of an infinite current-carrying wire inside a hollow conducting infinite cylinder, we can follow these steps:
Step 1: Understand the Magnetic Field Due to the Infinite Wire
The magnetic field B at a distance r from an infinite straight wire carrying a current I0 is given by Ampère's law:
B=μ0I02πr
where μ0 is the permeability of free space.
Step 2: Determine the Magnetic Field Inside the Cylinder
Since the hollow conducting cylinder carries a current I in the same direction as I0, the magnetic field inside the conducting cylinder (at radius r<R) will be the superposition of the fields due to both the wire and the cylinder. The magnetic field inside the cylinder is:
Bcylinder=μ0I2πr
Step 3: Calculate the Total Magnetic Field Inside the Cylinder
The total magnetic field Btotal at a distance r from the center (where r<R) is:
Btotal=B+Bcylinder=μ0I02πr+μ0I2πr=μ0(I0+I)2πr
Step 4: Calculate the Magnetic Pressure
The magnetic pressure PB is given by the formula:
PB=B22μ0
Thus, the magnetic pressure due to the total magnetic field is:
PB=12μ0(μ0(I0+I)2πr)2
=μ0(I0+I)28π2r2
Step 5: Calculate the Increment in Magnetic Pressure
The increment in magnetic pressure ΔPB due to the placement of the wire is the difference between the magnetic pressure with and without the wire.
1. Magnetic pressure without the wire (only the cylinder):
PB,cylinder=12μ0(μ0I2πr)2=μ0I28π2r2
2. Magnetic pressure with the wire:
PB,total=μ0(I0+I)28π2r2
Thus, the increment in magnetic pressure is:
ΔPB=PB,total−PB,cylinder=μ0(I0+I)28π2r2−μ0I28π2r2
=μ08π2r2((I0+I)2−I2)
=μ08π2r2(I20+2I0I)
Final Result
The increment in magnetic pressure due to the placement of the wire is:
ΔPB=μ0I20+2μ0I0I8π2r2
The magnetic field B at a distance r from an infinite straight wire carrying a current I0 is given by Ampère's law:
B=μ0I02πr
where μ0 is the permeability of free space.
Since the hollow conducting cylinder carries a current I in the same direction as I0, the magnetic field inside the conducting cylinder (at radius r<R) will be the superposition of the fields due to both the wire and the cylinder. The magnetic field inside the cylinder is:
Bcylinder=μ0I2πr
The total magnetic field Btotal at a distance r from the center (where r<R) is:
Btotal=B+Bcylinder=μ0I02πr+μ0I2πr=μ0(I0+I)2πr
The magnetic pressure PB is given by the formula:
PB=B22μ0
Thus, the magnetic pressure due to the total magnetic field is:
PB=12μ0(μ0(I0+I)2πr)2
=μ0(I0+I)28π2r2
The increment in magnetic pressure ΔPB due to the placement of the wire is the difference between the magnetic pressure with and without the wire.
PB,cylinder=12μ0(μ0I2πr)2=μ0I28π2r2
PB,total=μ0(I0+I)28π2r2
ΔPB=PB,total−PB,cylinder=μ0(I0+I)28π2r2−μ0I28π2r2
=μ08π2r2((I0+I)2−I2)
=μ08π2r2(I20+2I0I)
The increment in magnetic pressure due to the placement of the wire is:
ΔPB=μ0I20+2μ0I0I8π2r2
Similar Questions
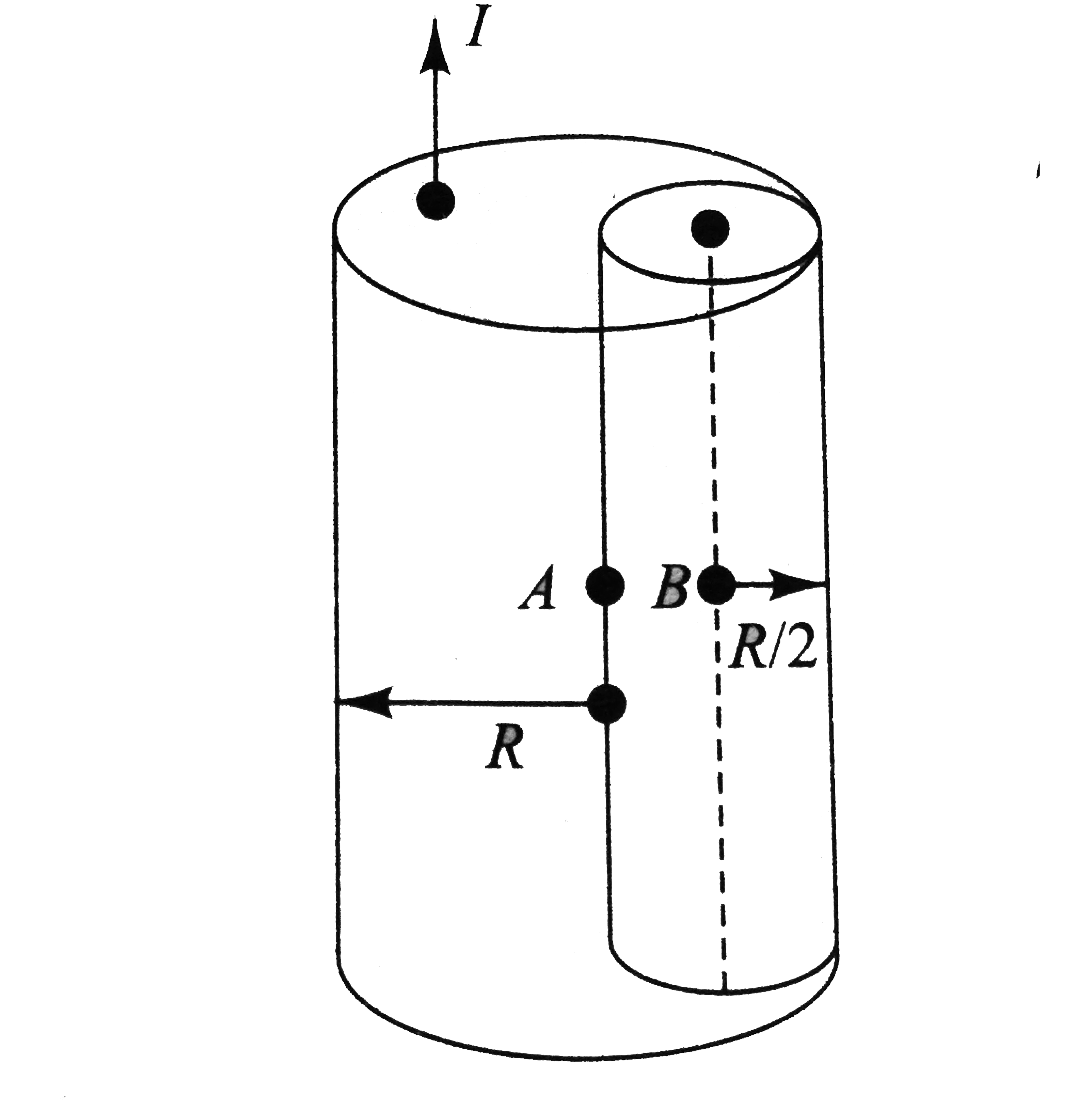
From a cylinder of radius R, a cylider of radius R/2 is removed, as shown in Fig. Current flowing in the remaining cylinder is I. Then, magnetic field strength is
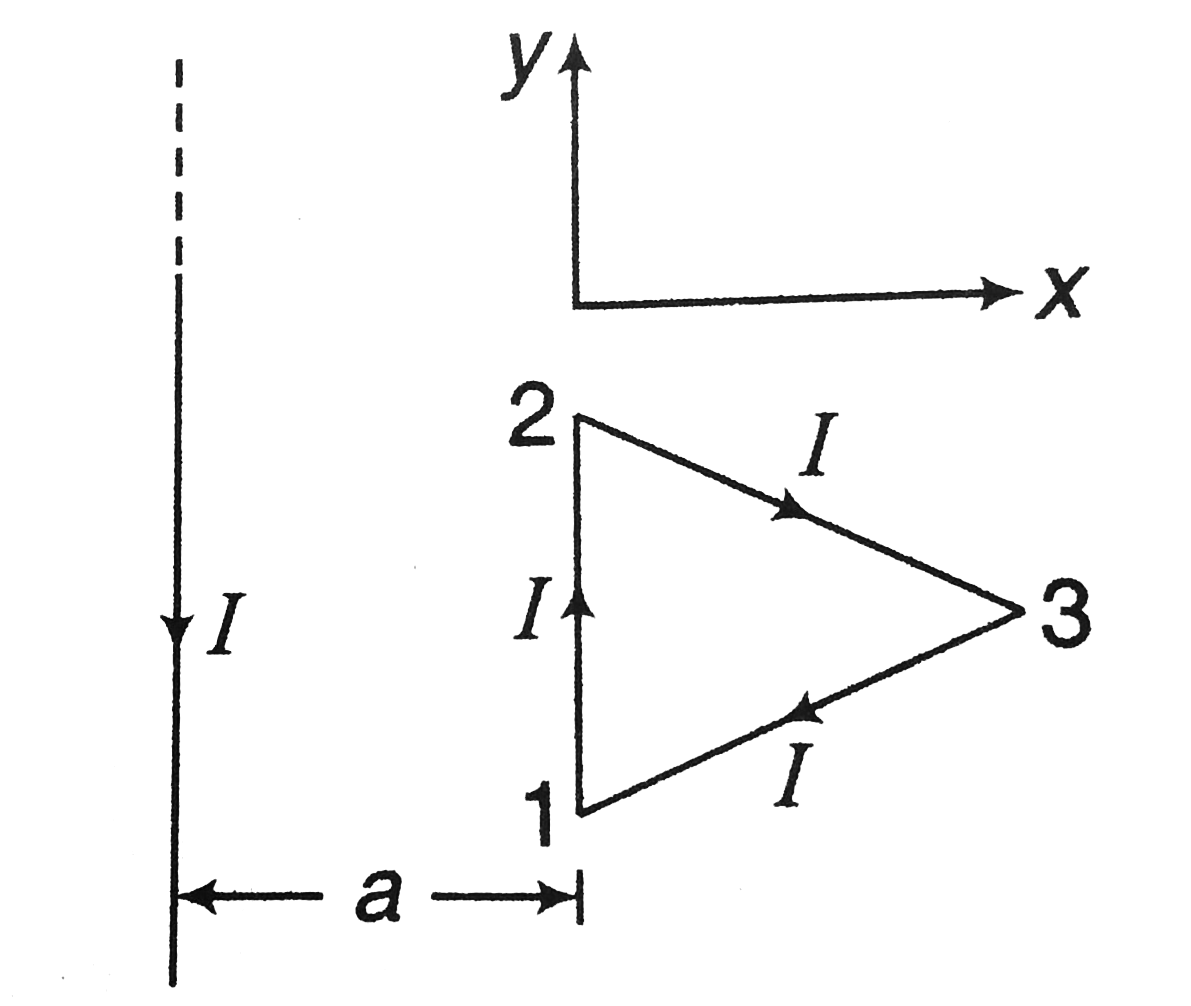
View SolutionAn equilateral triangular frame with side a carrying a current I is placed at a distance a from an infinitely long straight wire carrying a current I as shown in the figure. One side of the frame isparallel to the wire. The whole system lies in the xy-plane. Find the magnetic force F acting on the frame.
View SolutionShow a conduction loop placed near a long, straight wire carrying current i as shown. If the current increases continuously, find the direction of the induced current in the loop.

View SolutionAn infinitely long straight wire carrying a current I1 is partially surrounded by a loop as shown in Fig. The loop has a length L, radius R, and carries a current I2 The axis of the loop coincides with the wire. Calculate the force exerted on the loop.

View SolutionInfinite number of straight wires each carrying current I are equally placed as shown in the figure Adjacent wires have current in opposite direction Net magnetic field at point P is
 .
.
View SolutionAn infinitely long straight wire is carrying a current I1. Adjacent to it there is another equilateral triangular wire having current I2. Choose the wrong options
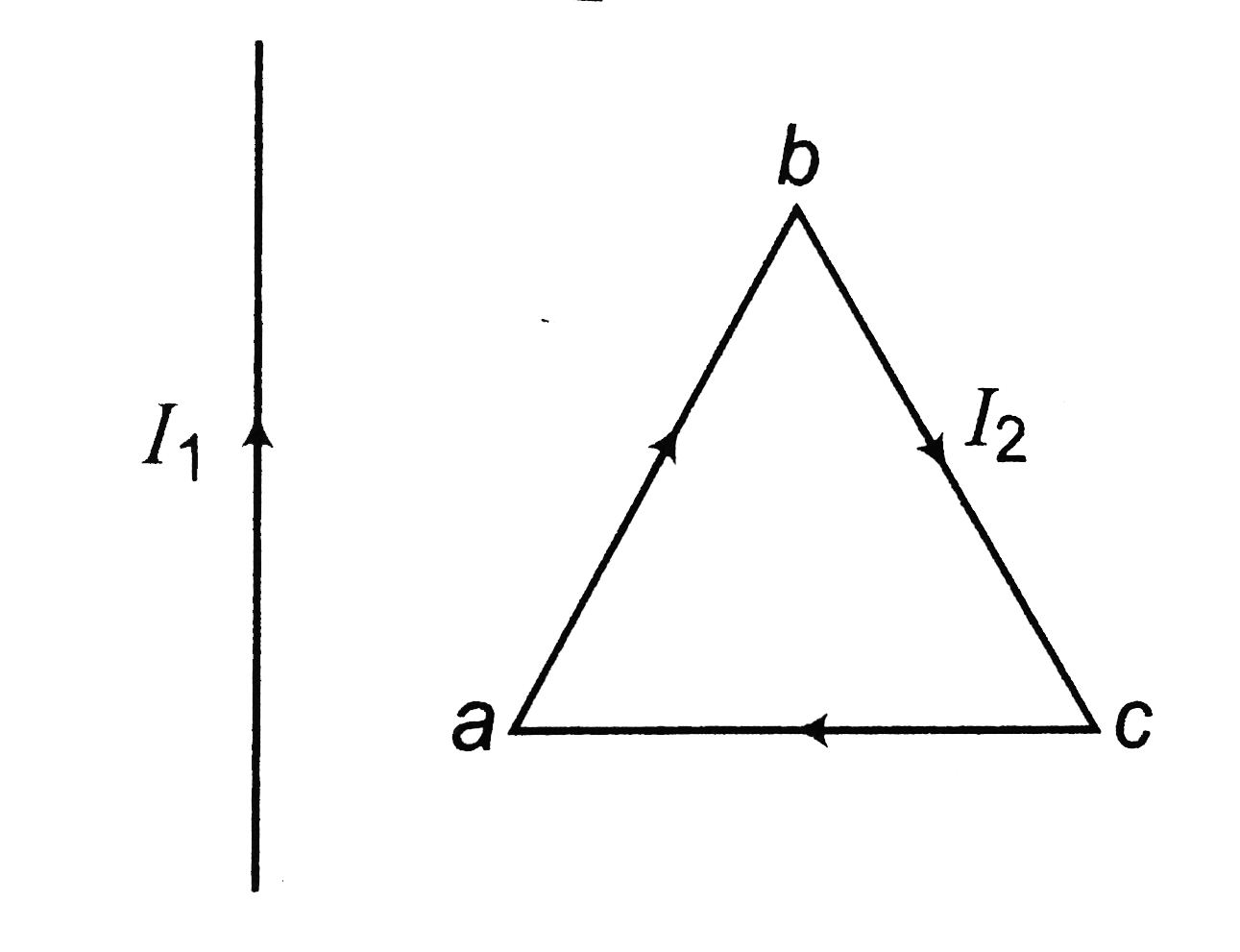
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

View SolutionAn infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
Graph between the magnetic field and radius is
View SolutionA rod CD of length b carrying a current l, is placed in a magnetic field due to a thin log wire AB carrying currrent I as shown in fig. Then find the net force experienced by the wire
View SolutionA conductor wire carrying current i is placed symmetrically and parallel to a long conducting sheet having a current per unit width j0 and width d, as shown in the figure. The force per unit length on the conductor wire will be
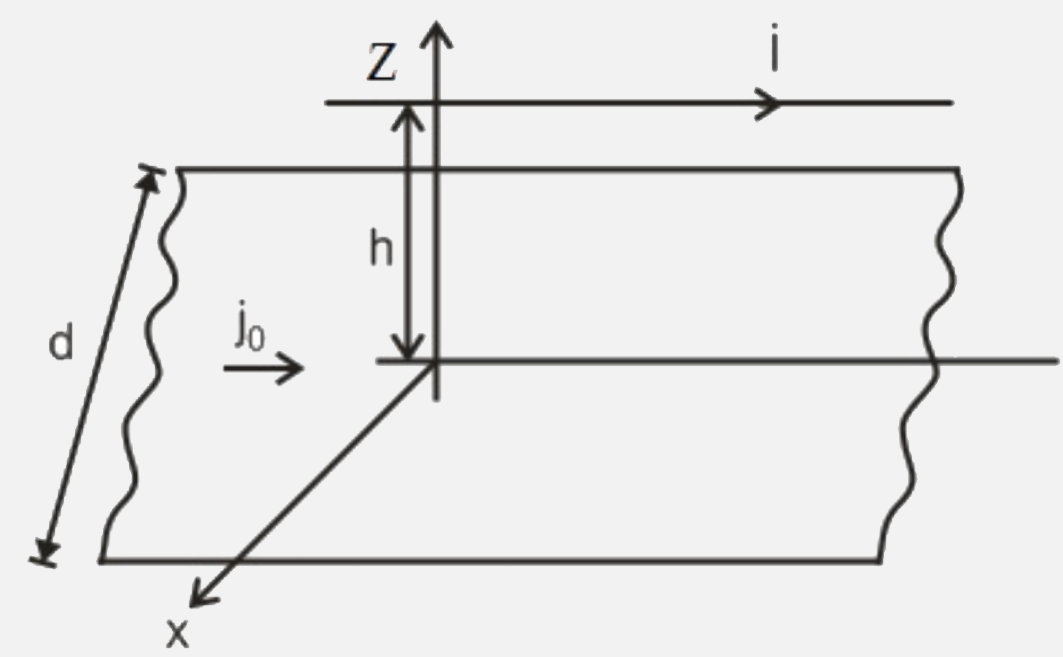
View Solution
