From a cylinder of radius R, a cylider of radius R/2 is removed, as shown in Fig. Current flowing in the remaining cylinder is I. Then, magnetic field strength is
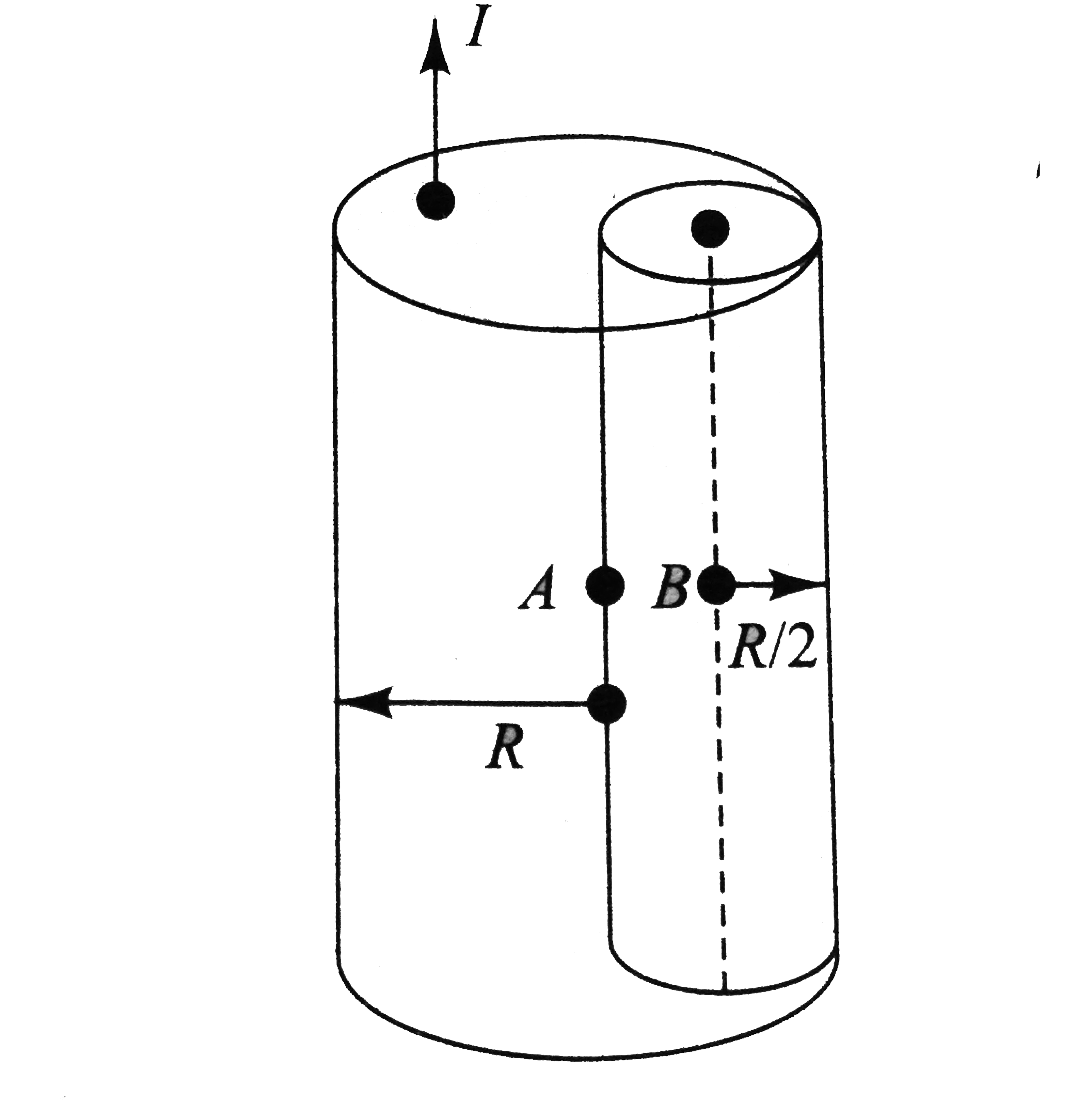
μ0I3πR at point B
μ0I2πR at point A
zero at point B
zero at point A
The correct Answer is:D
(d) Current density:ρ=1πR2−π(R/2)2⇒ρ=4I3πR2

Current in smaller cylinder (if there were): I1=ρπ(R2)2=I3
For A: BA=Bwhole-cylinder−Bsmall-cylinder
⇒BA=0−μ0(I3)2π(R/2)=−μ0I3πR
For B: BB=Bwhole -cylinder−Bsmall-cylinder
=μ0(I+I/3)(R/2)2πR2−0=μ0I3πR
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
From a cylinder of radius R, a cyclinder of radius R/2 is removed, as shown . Current flowing in the remaning cylinder is l. magnetic field strength is :

View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View Solution
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-
View SolutionWhat is moment of inertia of a cylinder of radius r, along its height?
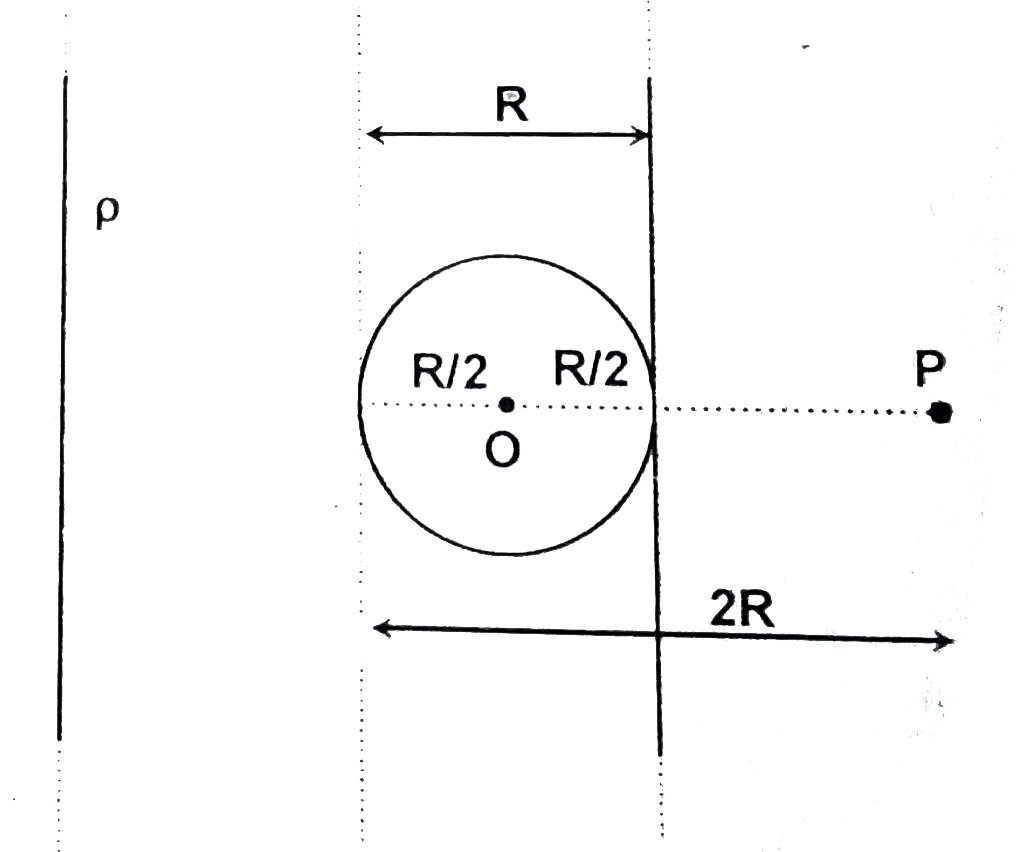
View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
View SolutionAn Infinite current carrying wire having current I0 is placed coaxially inside a hollow conducting infinite cylinder of radius R and having current I flowing along the length of the cylinder in the same direction as I0 what is the increment in magnetic pressure due to placing of the wire?
View SolutionA current carrying wire is placed in the grooves of an insulating semicircular disc of radius 'R', as shown in Fig. The current enters at point A and leaves from point B. Determine the magnetic field at Point D.
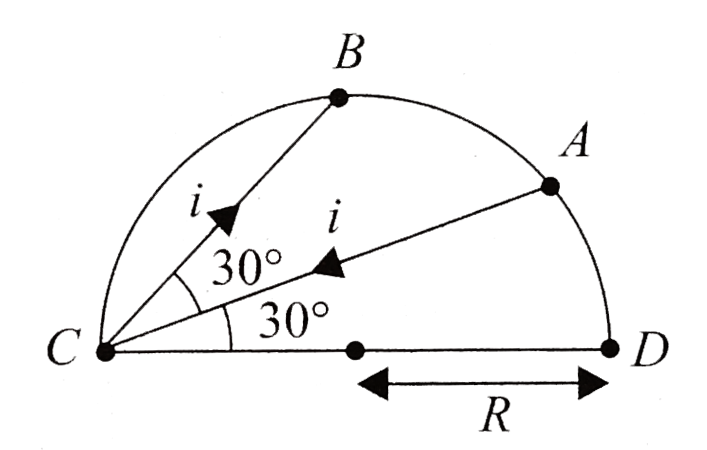
View SolutionA current carrying wire is placed in the grooves of an insulating semicircular disc of radius 'R', as shown in Fig. The current enters at point A and leaves from point B. Determine the magnetic field at Point D.

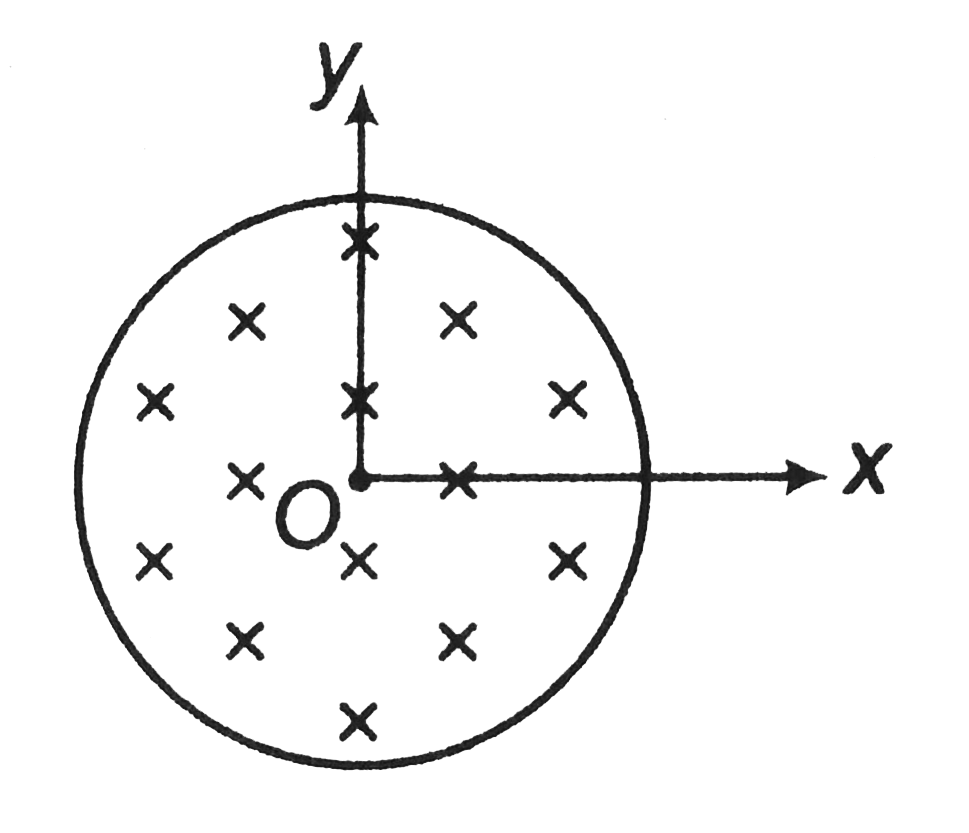
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
View Solution
A cylinder of radius R is to roll without slipping between two planks as shown in the figure. Then
View Solution
