The intensity of an electric field depends only on the co-ordinates x, y and z as follows:
unit.
The electrostatic energy stored between two imaginary concentric spherical shells of radii R and 2R with centre at origin is
The correct Answer is:C
To find the electrostatic energy stored between two concentric spherical shells of radii R and 2R, we can follow these steps:
Step 1: Understand the electric field
The electric field is given by:
→E=a(x^i+y^j+z^k)(x2+y2+z2)3/2
This can be expressed in terms of the position vector →r:
→E=a→r|→r|3
where |→r|=√x2+y2+z2.
Step 2: Calculate the energy density
The energy density u in an electric field is given by:
u=12ϵ0E2
Substituting the expression for E:
E=ar2(since |→r|=r)
Thus,
E2=(ar2)2=a2r4
Now, substituting this into the energy density formula:
u=12ϵ0a2r4
Step 3: Calculate the differential volume element
The differential volume element dv for a spherical shell is given by:
dv=4πr2dr
Step 4: Write the expression for differential energy
The differential energy du stored in the shell can be expressed as:
du=u⋅dv=12ϵ0a2r4⋅4πr2dr
This simplifies to:
du=2πϵ0a21r2dr
Step 5: Integrate to find total energy
To find the total energy U stored between the shells from r=R to r=2R, we integrate du:
U=∫2RRdu=∫2RR2πϵ0a21r2dr
Calculating the integral:
U=2πϵ0a2(−1r)2RR=2πϵ0a2(−12R+1R)
This simplifies to:
U=2πϵ0a2(1R−12R)=2πϵ0a2(12R)=πϵ0a2R
Final Result
Thus, the total electrostatic energy stored between the two spherical shells is:
U=πϵ0a2R
---
The electric field is given by:
→E=a(x^i+y^j+z^k)(x2+y2+z2)3/2
This can be expressed in terms of the position vector →r:
→E=a→r|→r|3
where |→r|=√x2+y2+z2.
The energy density u in an electric field is given by:
u=12ϵ0E2
Substituting the expression for E:
E=ar2(since |→r|=r)
Thus,
E2=(ar2)2=a2r4
Now, substituting this into the energy density formula:
u=12ϵ0a2r4
The differential volume element dv for a spherical shell is given by:
dv=4πr2dr
The differential energy du stored in the shell can be expressed as:
du=u⋅dv=12ϵ0a2r4⋅4πr2dr
This simplifies to:
du=2πϵ0a21r2dr
To find the total energy U stored between the shells from r=R to r=2R, we integrate du:
U=∫2RRdu=∫2RR2πϵ0a21r2dr
Calculating the integral:
U=2πϵ0a2(−1r)2RR=2πϵ0a2(−12R+1R)
This simplifies to:
U=2πϵ0a2(1R−12R)=2πϵ0a2(12R)=πϵ0a2R
Thus, the total electrostatic energy stored between the two spherical shells is:
U=πϵ0a2R
Similar Questions
The intensity of an electric field depends only on the coordinates x and y as follows,
E=a(xˆi+yˆj)x2+y2 where, a is constant and ˆi and ˆj are the unit vectors of the x and y axes. Find the charges within a sphere of radius R with the centre at the origin.View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionThe electric field strength depends only on the x, y, and z coordinates according to the law E=a(xˆi+yˆj+zˆk)(x2+y2+z2)3/2, where a=280Nm2C−1 is a constant. If the potential difference between (3,2,6) and (0,3,4) is x2. What is the value of x.
View SolutionA metal sphere of radius R is charged to a pontital V . (a ) Find the electrostatic energy stored in the electric field within a concentric sphere of radius 2 R . (b )Show that the electrostatic field energy stored outside the sphere of radius 2R equals that stored within it .
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionA point charge Q is placed at the origin of the coordinate system. What is the electrostatic energy within an annular spherical region, with centre at origin and inner and outer radii R and 2R respectively.
View SolutionFind the angle between the two lines 2x=3y=−zand6x=−y=−4z.
View SolutionFind the values of x,y and z so that the vectors →a=xˆi+2ˆj+zˆkand→b=2ˆi+yˆj+ˆk are equal.
View SolutionThree concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
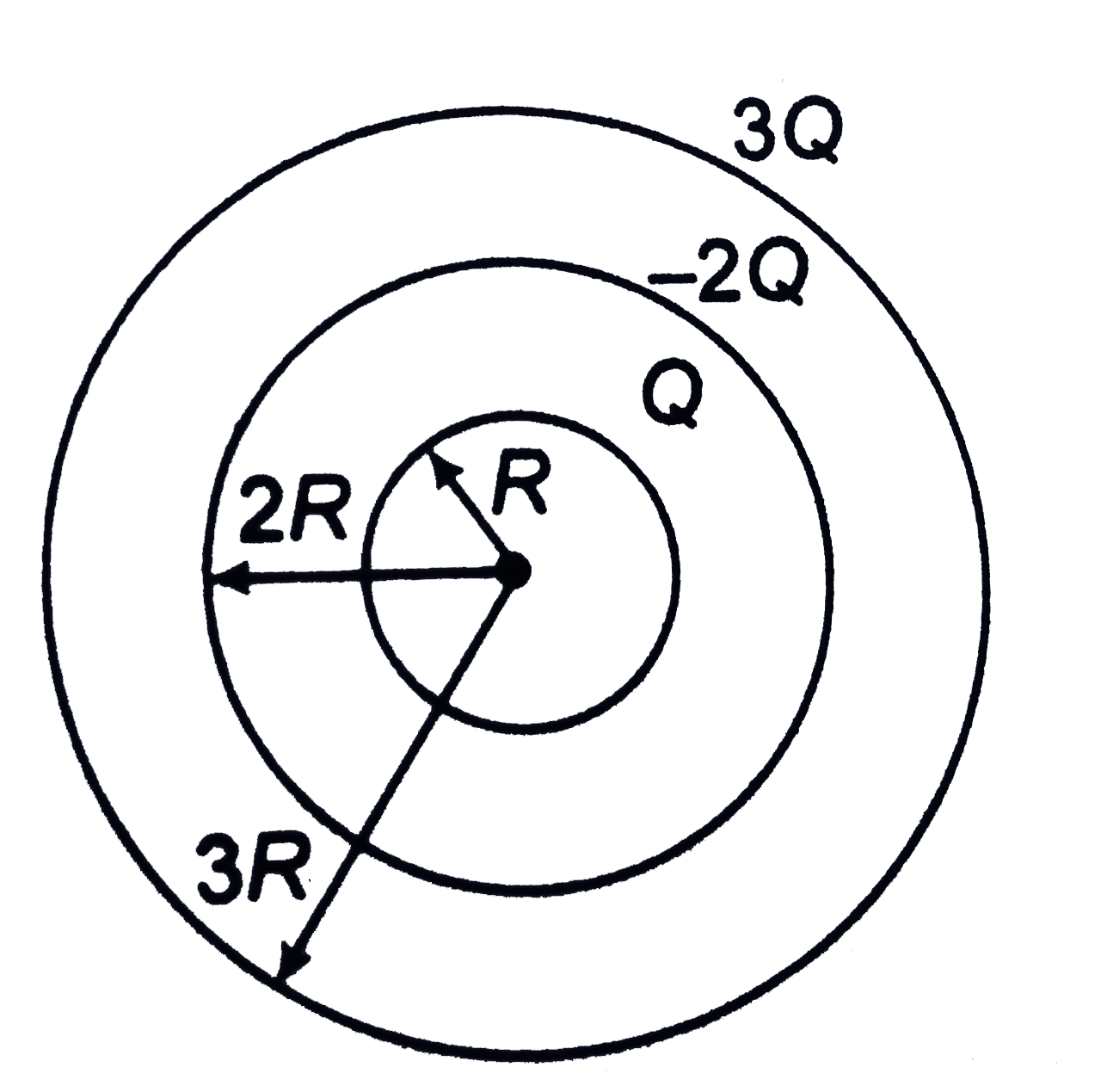
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre . b. Compute the electric field at r=52R
c. Compute the total electrostatic energy stored in the system.
The inner shell is now connected to the external one by a conducting wire, passing through a very small hole in the middle shell.
d. Compute the charges on the spheres of radii R and 3R.
e. Compute the electric field at r=52RView Solution

