Three concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
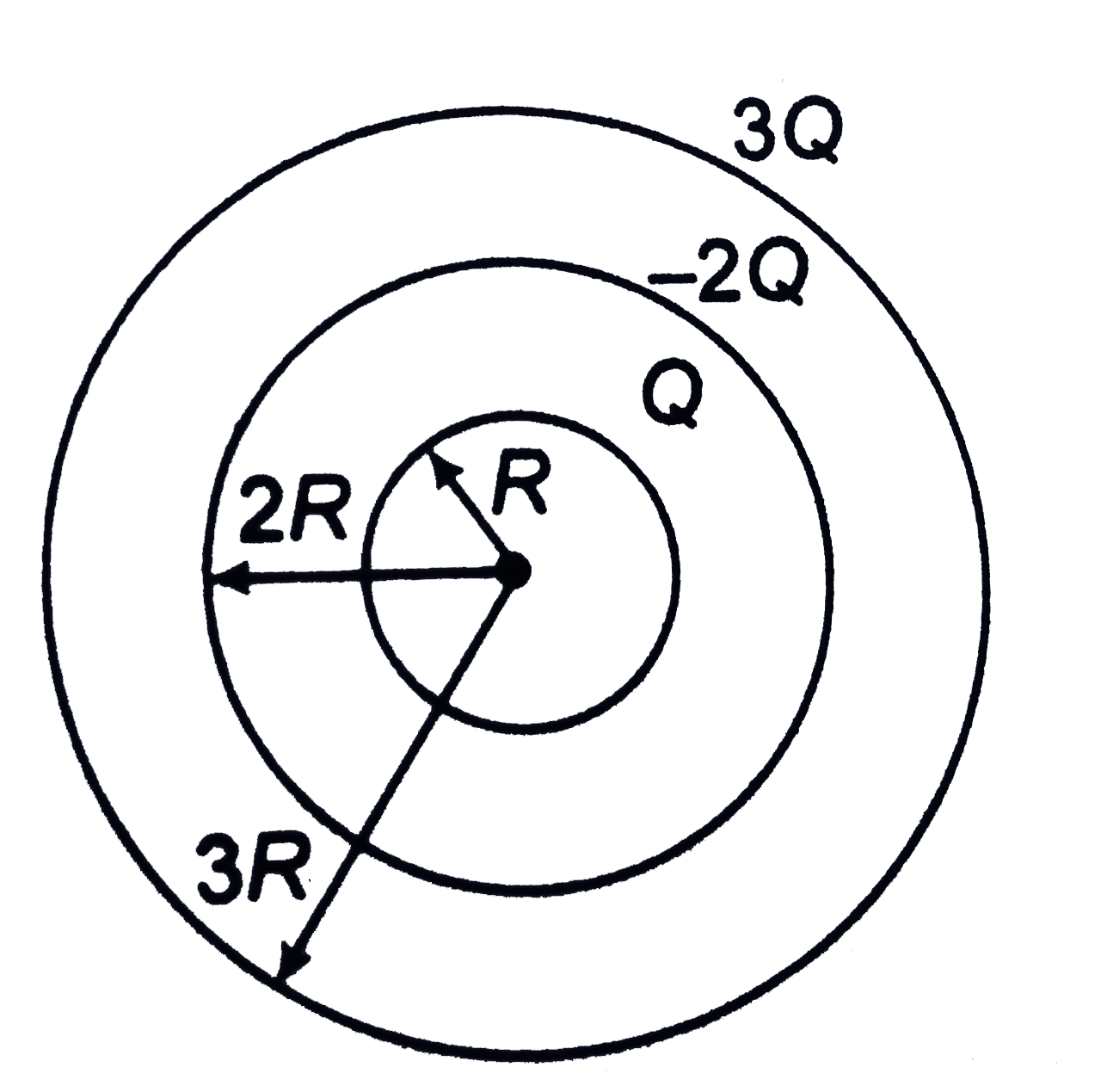
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre
. b. Compute the electric field at r=52R
c. Compute the total electrostatic energy stored in the system.
The inner shell is now connected to the external one by a conducting wire, passing through a very small hole in the middle shell.
d. Compute the charges on the spheres of radii R and 3R.
e. Compute the electric field at r=52R
The correct Answer is:A, B, C
a. At r=R,
V=14πε0[QR−2Q2R+3Q3R]
=(14πε0)(QR)
Atr=3R
V=14πε0[Q3R−2Q3R+3Q3R]=Q6πε0R
b. E=(14πε0(qinr2)
=(14πε0)[Q−2Q(5R/2)]=−Q25πε0R2
Minus sign implies that this electric field is radialy towards centre.
c. 
UT=U1+U2+U3
whereU1=12Q2C1
whereC1=(4πε0)/(1R−12R)
U2=12Q2C2
where, C2=4πε0/(12R−13R)
and U3=12(2Q)2C3
where C3=4πε0/(13R−1∞) d. 
total charge on (A+C) is 3Q+Q=3Q
Now, VA=VC
∴kqR−k(2Q)2R=k(4Q−q)3R
=k(Q−2Q+3Q)3R
solving this equation we get
q=Q2
Now, qA=q=Q2
qC=4Q−q=72Q
e. E=14πε0.qinr2=14πε0⎡⎢
⎢
⎢⎣q−2Q(5R2)2⎤⎥
⎥
⎥⎦=−3Q50πepslon0R2 Minus sign indicates that electric field is radially inwards.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE6videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.110videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Objective82videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Three concentric conducting spherical shells of radii R,2R carry charges Q, -2Q and 3Q, respectively. Find the electric potential at r = R and at r = 3 R, where r is the radii distance from the centre.
 View Solution
View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R
 View Solution
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
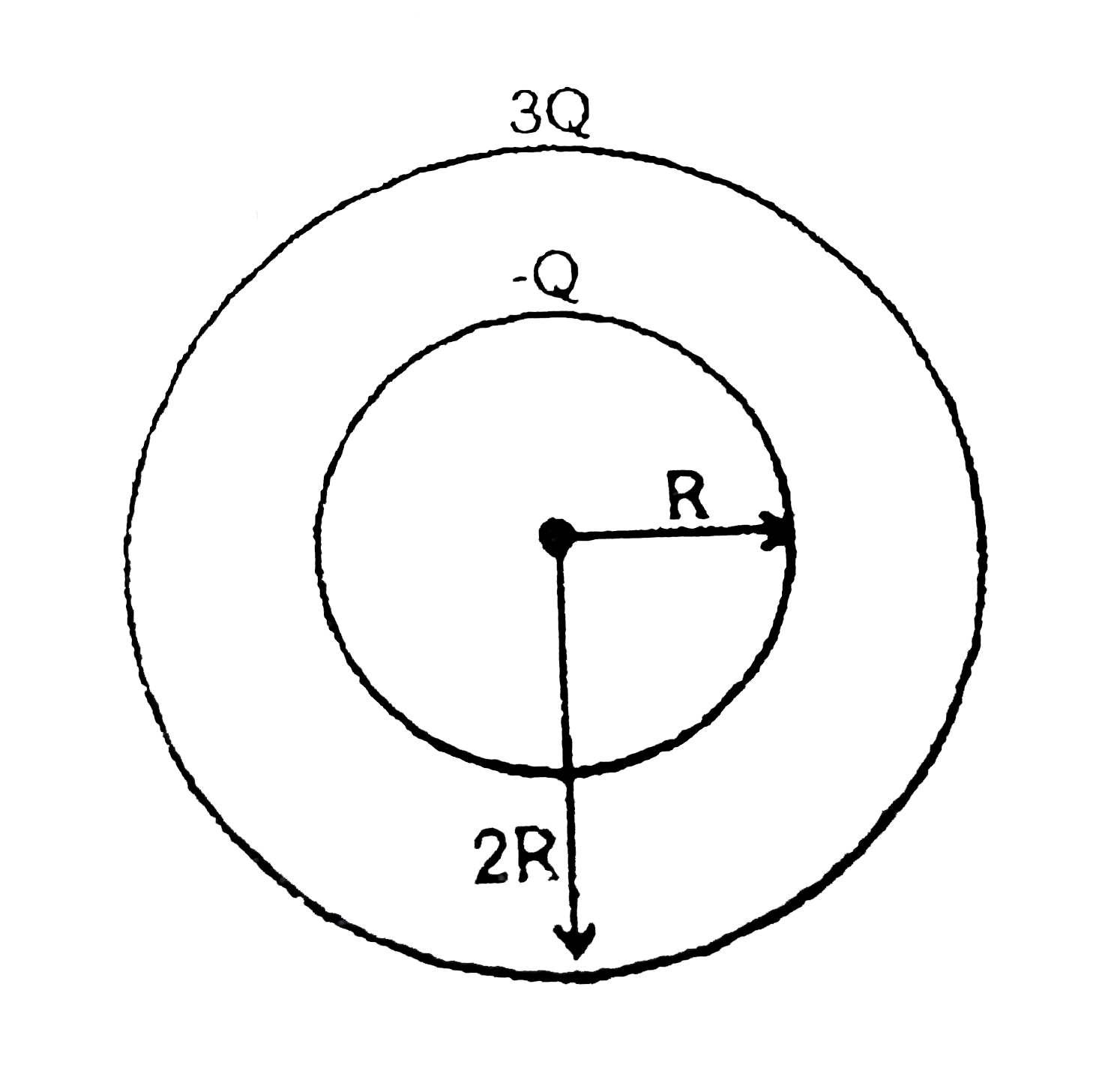
View SolutionTwo conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
 View Solution
View SolutionTwo concentric conducting thin shells of radius R and 2 R carry charges +Q and +3Q respectively. The magnitude of electric field at a distance x outside and inside from the surface of outer sphere is same. Then the value of x is
 View Solution
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
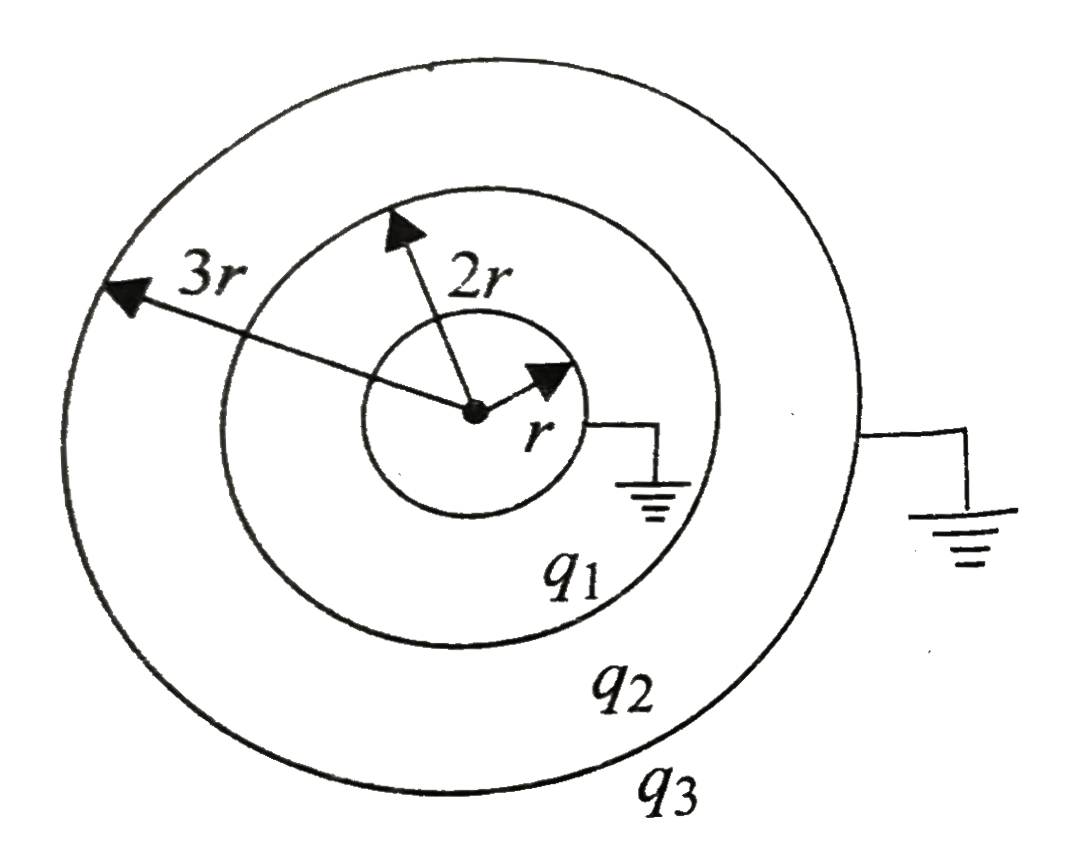
View SolutionThree concentric conducting spherical shells have radii r, 2r, and 3r and charges q1,q2andq3, respectively. Innermost and outermost shells are earthed as shown in figure. The charges shown are after earthing. Select the correct alternative.
 View Solution
View SolutionTwo concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View Solution

