The intensity of an electric field depends only on the coordinates x and y as follows,
where, a is constant and and are the unit vectors of the x and y axes. Find the charges within a sphere of radius R with the centre at the origin.
The correct Answer is:A, D
To find the charge within a sphere of radius R centered at the origin, given the electric field intensity E=a(x^i+y^j)x2+y2, we will follow these steps:
Step 1: Understand the Electric Field
The electric field E is given in terms of coordinates x and y. It is a vector field that depends on the position in the xy-plane.
Step 2: Define the Surface Area Element
For a sphere of radius R, we need to define a small area vector dS on the surface of the sphere. The area vector dS is directed radially outward and can be expressed as:
d→S=dS^n
where ^n is the unit normal vector to the surface of the sphere. In spherical coordinates, this can be expressed as:
^n=x^i+y^j+z^kR
Step 3: Calculate the Electric Flux
The electric flux ΦE through the surface of the sphere is given by the integral of the electric field over the surface area:
ΦE=∫S→E⋅d→S
Substituting the expressions for →E and d→S:
ΦE=∫Sa(x^i+y^j)x2+y2⋅dS^n
This simplifies to:
ΦE=∫Sa(x^i+y^j)x2+y2⋅(x^i+y^j+z^kRdS)
Step 4: Simplify the Dot Product
The dot product →E⋅^n is:
→E⋅^n=aR(x2+y2x2+y2)=aR
Thus, the flux becomes:
ΦE=∫SaRdS
Step 5: Calculate the Total Surface Area of the Sphere
The total surface area A of the sphere is:
A=4πR2
Therefore, the total electric flux is:
ΦE=aR⋅4πR2=4πaR
Step 6: Use Gauss's Law to Find the Enclosed Charge
According to Gauss's Law, the electric flux through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
ΦE=Qϵ0
Setting the two expressions for flux equal gives:
4πaR=Qϵ0
Thus, the charge enclosed Q is:
Q=4πaRϵ0
Final Answer
The charge within a sphere of radius R centered at the origin is:
Q=4πaRϵ0
The electric field E is given in terms of coordinates x and y. It is a vector field that depends on the position in the xy-plane.
For a sphere of radius R, we need to define a small area vector dS on the surface of the sphere. The area vector dS is directed radially outward and can be expressed as:
d→S=dS^n
where ^n is the unit normal vector to the surface of the sphere. In spherical coordinates, this can be expressed as:
^n=x^i+y^j+z^kR
The electric flux ΦE through the surface of the sphere is given by the integral of the electric field over the surface area:
ΦE=∫S→E⋅d→S
Substituting the expressions for →E and d→S:
ΦE=∫Sa(x^i+y^j)x2+y2⋅dS^n
This simplifies to:
ΦE=∫Sa(x^i+y^j)x2+y2⋅(x^i+y^j+z^kRdS)
The dot product →E⋅^n is:
→E⋅^n=aR(x2+y2x2+y2)=aR
Thus, the flux becomes:
ΦE=∫SaRdS
The total surface area A of the sphere is:
A=4πR2
Therefore, the total electric flux is:
ΦE=aR⋅4πR2=4πaR
According to Gauss's Law, the electric flux through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
ΦE=Qϵ0
Setting the two expressions for flux equal gives:
4πaR=Qϵ0
Thus, the charge enclosed Q is:
Q=4πaRϵ0
The charge within a sphere of radius R centered at the origin is:
Q=4πaRϵ0
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
The intensity of an electric field depends only on the co-ordinates x, y and z as follows:
→E=a(xˆi+yˆj+zˆk)(x2+y2+z2)3/2unit.
The electrostatic energy stored between two imaginary concentric spherical shells of radii R and 2R with centre at origin isView SolutionThe work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
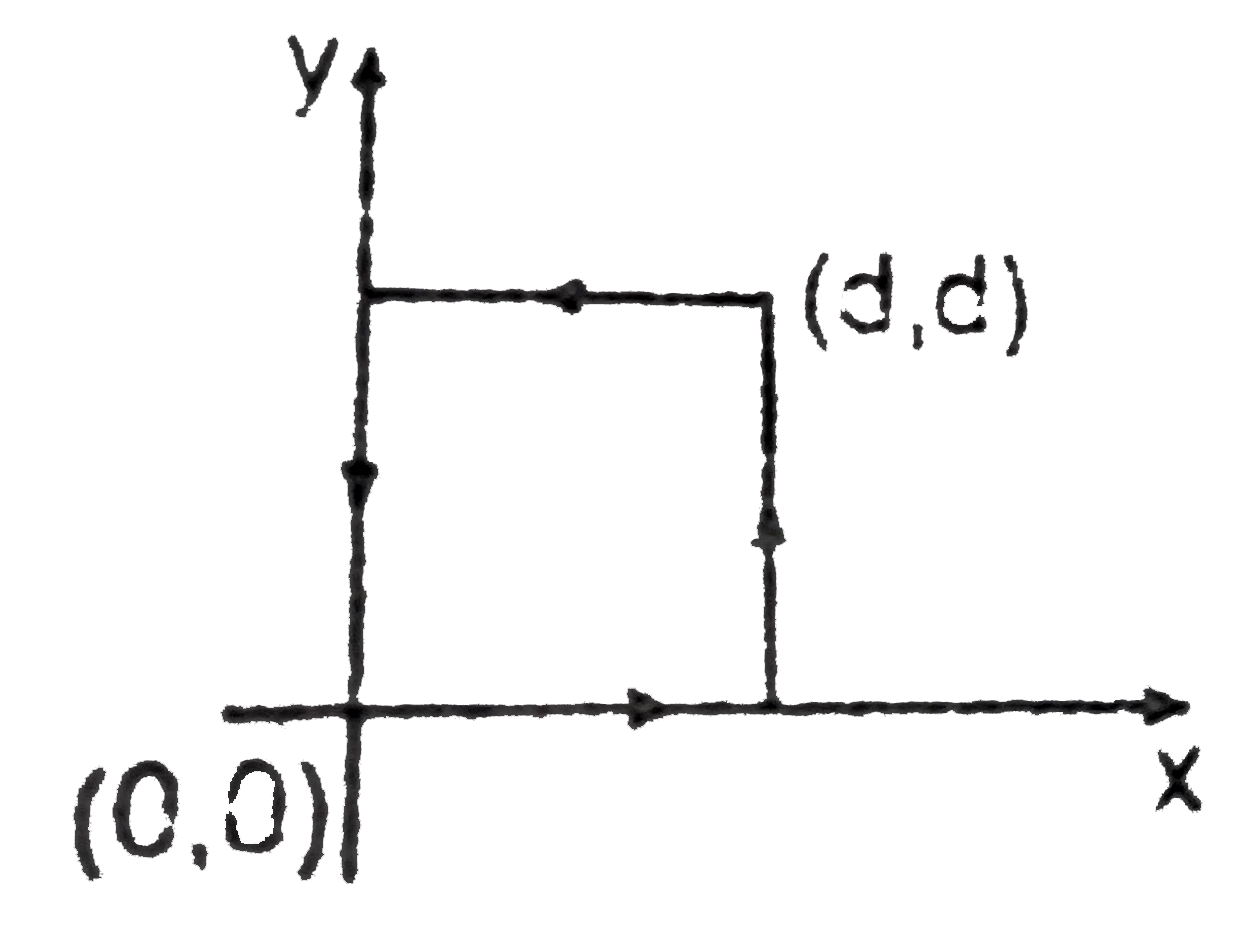 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
If ˆi,ˆj and ˆk are unit vectors along X,Y & Z axis respectively, then what is the magnitude of ˆi+ˆj+ˆk
View SolutionA particle projected from origin moves in x-y plane with a velocity →v=3ˆi+6xˆj, where ˆi and ˆj are the unit vectors along x and y axis. Find the equation of path followed by the particle :-
View SolutionIf ˆi and ˆj are unit vectors along X-and Y-axis respectively, then what is the magnitude and direction of ˆi+ˆj and ˆi−ˆj ?
View SolutionIf ˆi,ˆj and ˆk are unit vectors along X,Y & Z axis respectively, then tick the wrong statement:
View SolutionThe electric field strength depends only on the x, y, and z coordinates according to the law E=a(xˆi+yˆj+zˆk)(x2+y2+z2)3/2, where a=280Nm2C−1 is a constant. If the potential difference between (3,2,6) and (0,3,4) is x2. What is the value of x.
View SolutionDetermine the electric field strength vector if the potential of this field depends on x, coordinates as
(a) V=a(x2—y2) (b) V=axy
where, a is a constant.View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
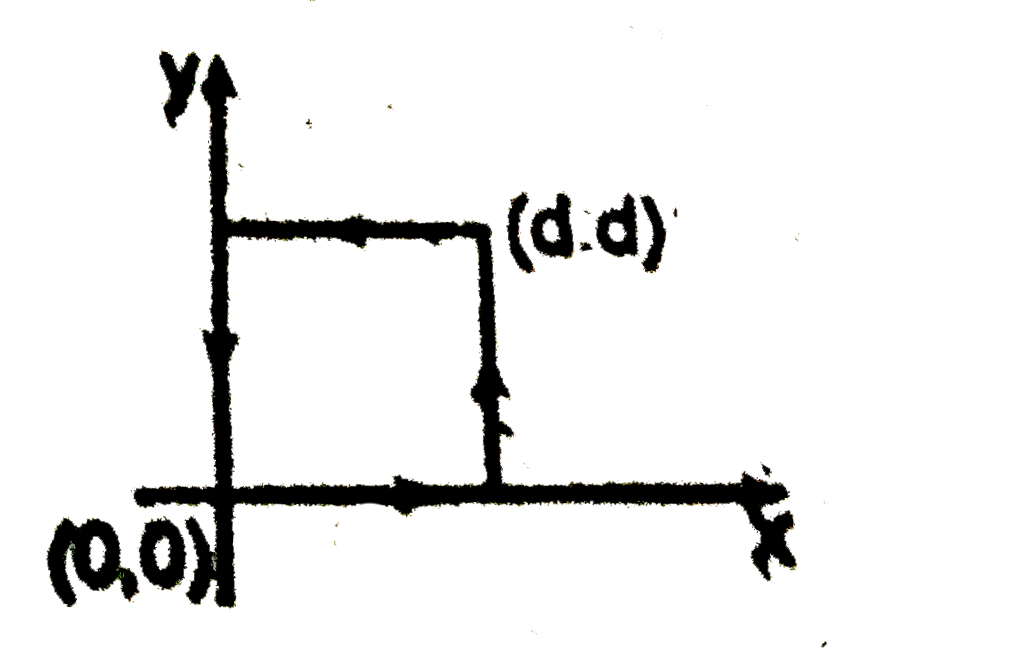 View Solution
View Solution

