A space charge of density ρ is uniformly distributed in an infinitely long cylinder of radius R Then, for any point at distance r from the axis (relative permittivity = 1)
the electric field is E=ρr2∈0 for 0 < r < R
the electric field is E=ρR32∈0r2 for r > R
the electric field is E=ρr∈0 for 0 < r < R
the electric field is E=ρR2∈0r for r > R
The correct Answer is:A
To solve the problem of finding the electric field inside and outside an infinitely long cylinder with a uniform space charge density ρ, we will apply Gauss's law.
1. Identify the Geometry and Charge Distribution:
- We have an infinitely long cylinder with radius R and a uniform charge density ρ. We need to find the electric field at a distance r from the axis of the cylinder.
2. Consider the Case Inside the Cylinder (r<R):
- For points inside the cylinder, we will use a Gaussian surface in the form of a cylinder of radius r (where r<R) and length L.
- The electric field E is assumed to be uniform and radial due to symmetry.
3. Apply Gauss's Law:
- According to Gauss's law, the electric flux through the Gaussian surface is equal to the charge enclosed divided by ϵ0:
ΦE=E⋅A=E⋅(2πrL)
- The charge enclosed Qenc within the Gaussian surface is given by:
Qenc=ρ⋅V=ρ⋅(πr2L)
- Thus, Gauss's law gives us:
E⋅(2πrL)=ρ⋅(πr2L)ϵ0
4. Solve for the Electric Field Inside the Cylinder:
- Cancel L and π from both sides:
E⋅(2r)=ρr2ϵ0
- Rearranging gives:
E=ρr2ϵ0
5. Consider the Case Outside the Cylinder (r>R):
- For points outside the cylinder, we will again use a Gaussian surface in the form of a cylinder of radius r (where r>R).
- The charge enclosed is the total charge of the cylinder up to radius R:
Qenc=ρ⋅(πR2L)
- Using Gauss's law, we have:
E⋅(2πrL)=ρ⋅(πR2L)ϵ0
6. Solve for the Electric Field Outside the Cylinder:
- Cancel L and π from both sides:
E⋅(2r)=ρR2ϵ0
- Rearranging gives:
E=ρR22ϵ0r
Summary of Results:
- Electric Field Inside the Cylinder (r<R):
E=ρr2ϵ0
- Electric Field Outside the Cylinder (r>R):
E=ρR22ϵ0r
- We have an infinitely long cylinder with radius R and a uniform charge density ρ. We need to find the electric field at a distance r from the axis of the cylinder.
- For points inside the cylinder, we will use a Gaussian surface in the form of a cylinder of radius r (where r<R) and length L.
- The electric field E is assumed to be uniform and radial due to symmetry.
- According to Gauss's law, the electric flux through the Gaussian surface is equal to the charge enclosed divided by ϵ0:
ΦE=E⋅A=E⋅(2πrL)
- The charge enclosed Qenc within the Gaussian surface is given by:
Qenc=ρ⋅V=ρ⋅(πr2L)
- Thus, Gauss's law gives us:
E⋅(2πrL)=ρ⋅(πr2L)ϵ0
- Cancel L and π from both sides:
E⋅(2r)=ρr2ϵ0
- Rearranging gives:
E=ρr2ϵ0
- For points outside the cylinder, we will again use a Gaussian surface in the form of a cylinder of radius r (where r>R).
- The charge enclosed is the total charge of the cylinder up to radius R:
Qenc=ρ⋅(πR2L)
- Using Gauss's law, we have:
E⋅(2πrL)=ρ⋅(πR2L)ϵ0
- Cancel L and π from both sides:
E⋅(2r)=ρR2ϵ0
- Rearranging gives:
E=ρR22ϵ0r
- Electric Field Inside the Cylinder (r<R):
E=ρr2ϵ0
- Electric Field Outside the Cylinder (r>R):
E=ρR22ϵ0r
Similar Questions
Electric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View Solution
Knowledge Check
Let ρ(r)=QrπR4 be the charge density distribution for a soild sphere of radius R and total charge Q. For a point P inside the sphere at a distance r1 from the centre of the sphere, the magnitude of electric field is
AQr214πε0R4BQr213πε0R4C0DQ4iε0r21
Let P(r)=QπR4r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is:
View SolutionConsider an atom with atomic number Z as consisting of a positive point charge at the centre and surrounded by a distribution of negative electricity uniformly distributed within a sphere of radius R. The electric field at a point inside the atom at a distance r from the centre is
View SolutionFigure shows the cross-sectional view of the hollow cylindrical conductor with inner radius 'R' and outer radius '2R', cylinder carrying uniformly distributed current along it's axis. The magnetic induction at point 'P' at a distance 3R2 from the axis of the cylinder will be
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
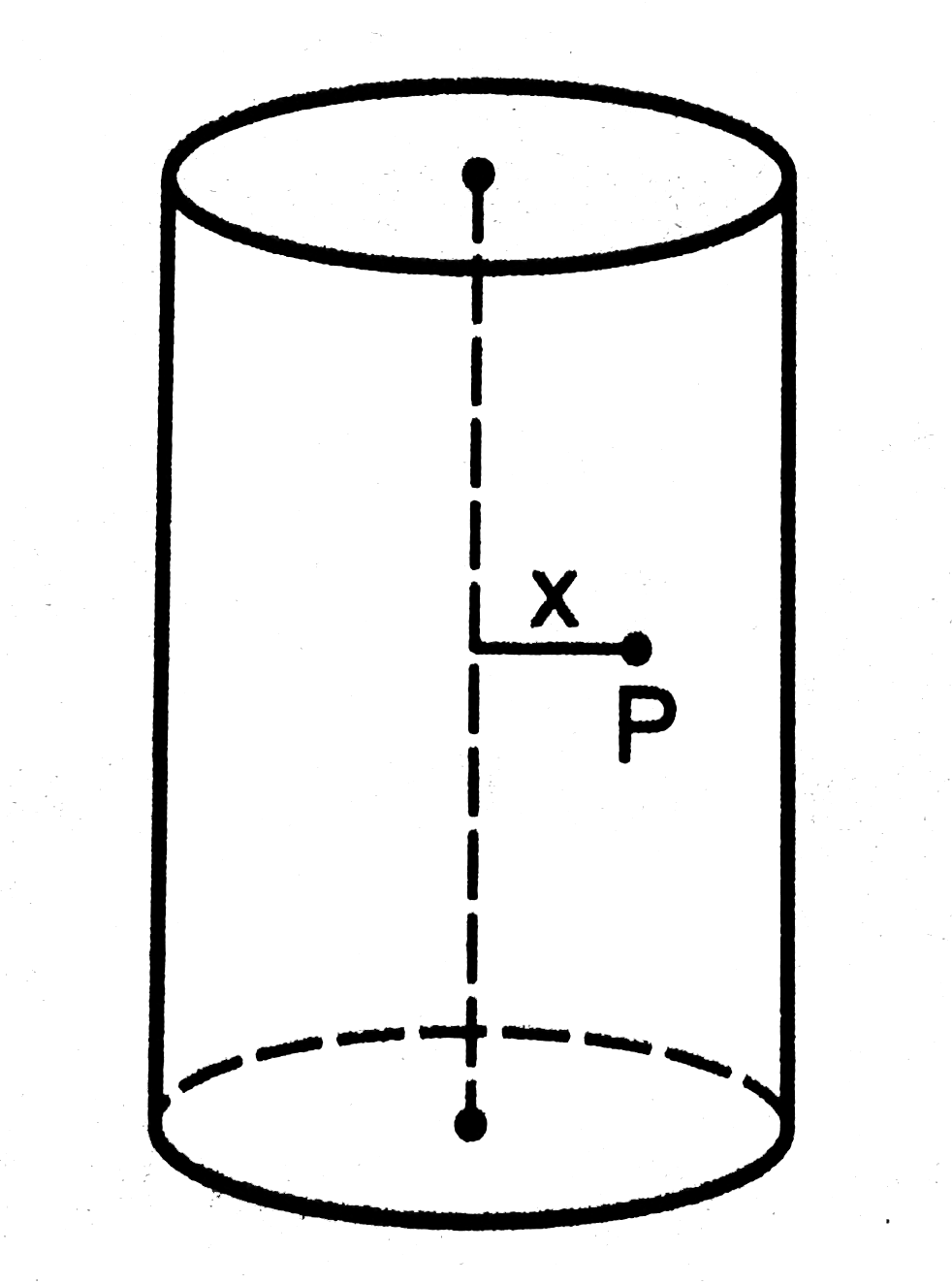
View SolutionA long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
View Solution
