In an circuit consisting of resistance and inductance , the voltage across is volt and that across is volt.The total voltage across the combination is
The correct Answer is:C
To solve the problem, we need to find the total voltage across a combination of resistance (R) and inductance (L) in an AC circuit. The voltages across the resistor (V_R) and the inductor (V_L) are given as follows:
- Voltage across the resistor, VR=60V
- Voltage across the inductor, VL=80V
Step 1: Understand the relationship between voltages in an R-L circuit
In an R-L circuit, the total voltage (V) across the combination is given by the vector sum of the voltages across the resistor and the inductor. This is because the voltages are not in phase; the voltage across the resistor is in phase with the current, while the voltage across the inductor lags the current by 90 degrees.
Step 2: Use the Pythagorean theorem
The total voltage can be calculated using the Pythagorean theorem:
V=√V2R+V2L
Step 3: Substitute the values
Now, we substitute the given values into the equation:
V=√(60V)2+(80V)2
Step 4: Calculate V2R and V2L
Calculating the squares:
V2R=602=3600V2
V2L=802=6400V2
Step 5: Add the squares
Now, add these two results:
V2R+V2L=3600+6400=10000V2
Step 6: Take the square root
Finally, we take the square root to find the total voltage:
V=√10000=100V
Conclusion
The total voltage across the combination of resistance and inductance is:
100V
- Voltage across the inductor, VL=80V
In an R-L circuit, the total voltage (V) across the combination is given by the vector sum of the voltages across the resistor and the inductor. This is because the voltages are not in phase; the voltage across the resistor is in phase with the current, while the voltage across the inductor lags the current by 90 degrees.
The total voltage can be calculated using the Pythagorean theorem:
V=√V2R+V2L
Now, we substitute the given values into the equation:
V=√(60V)2+(80V)2
Calculating the squares:
V2R=602=3600V2
V2L=802=6400V2
Now, add these two results:
V2R+V2L=3600+6400=10000V2
Finally, we take the square root to find the total voltage:
V=√10000=100V
The total voltage across the combination of resistance and inductance is:
100V
Topper's Solved these Questions
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -2 Part-1
Explore 14 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:Exercise -2 Part-2
Explore 6 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:HIGH LEVEL PROBLEMS
Explore 11 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
Similar Questions
A 20volts AC is applied to a circuit consisting of a resistance and a coil with negligible resistance. If the voltage across the resistance is 12V, the voltage across the coil is
View SolutionIn an LCR series ac circuit , the voltage across each of the components , L,C and R is 50 V . The voltage across the LC combination will be :
View SolutionIn an L-C-R circuit the AC voltage across R, L and C comes out as 10 V , 10 V and 20 V respectively . The voltage across the enter combination will be
View SolutionA coil of resistance R and inductance L is connected across an a.c power supply of r.m.s. voltage V. The average power dissipated in the coil is,
View SolutionIn the given circuit , the voltage across the base emitter junction is
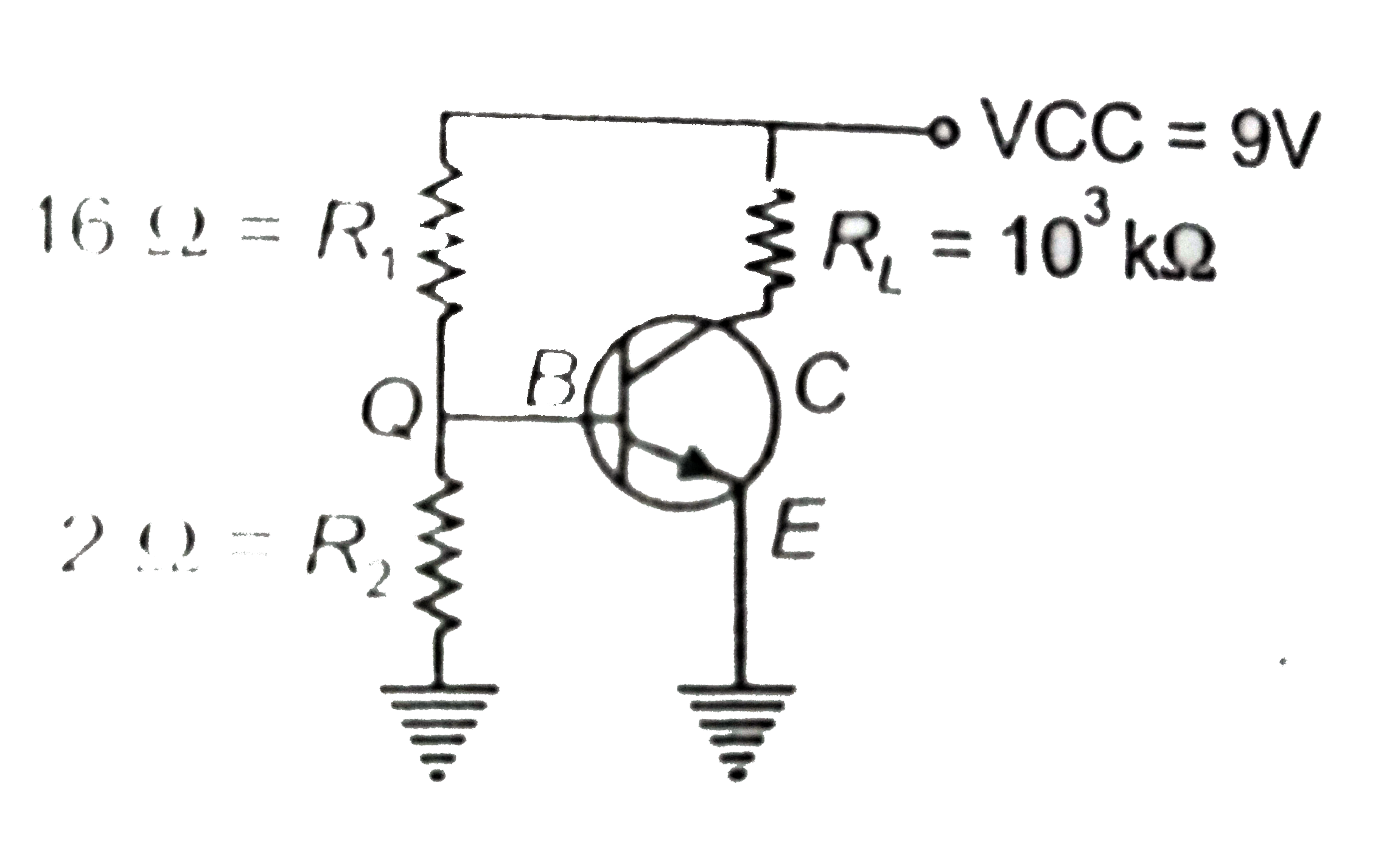
View SolutionAn alternating voltage is connected in series with a resistance R and inductance L if the potential drop across the resistance is 200V and across the inductance is 150V, then the applied voltage is
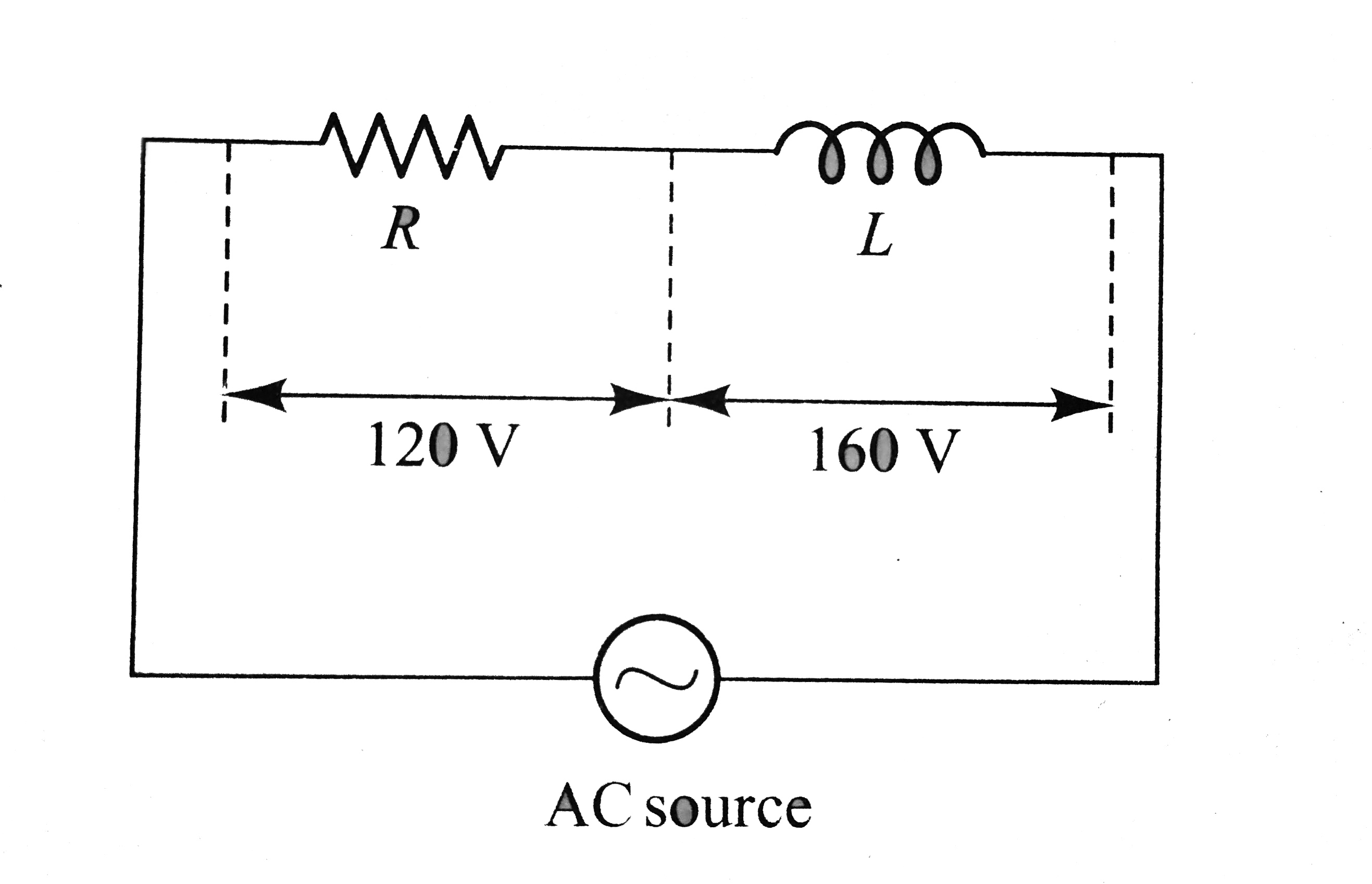
View SolutionThe circuit given in fig. has a resistanceless choke coil L and a resistance R. The voltage across R and L are also given in the figure. The virtual value of the applied voltage is
View SolutionIn a series resonant circuit, the ac, voltage across resistance R, inductance L and capacitance are 5V, 10V and 10V, respectively. The ac. voltage applied to the circuit will be
View SolutionIn series LCR circuit, the voltages across R, L and C are shown in the figure. The voltage of applied source
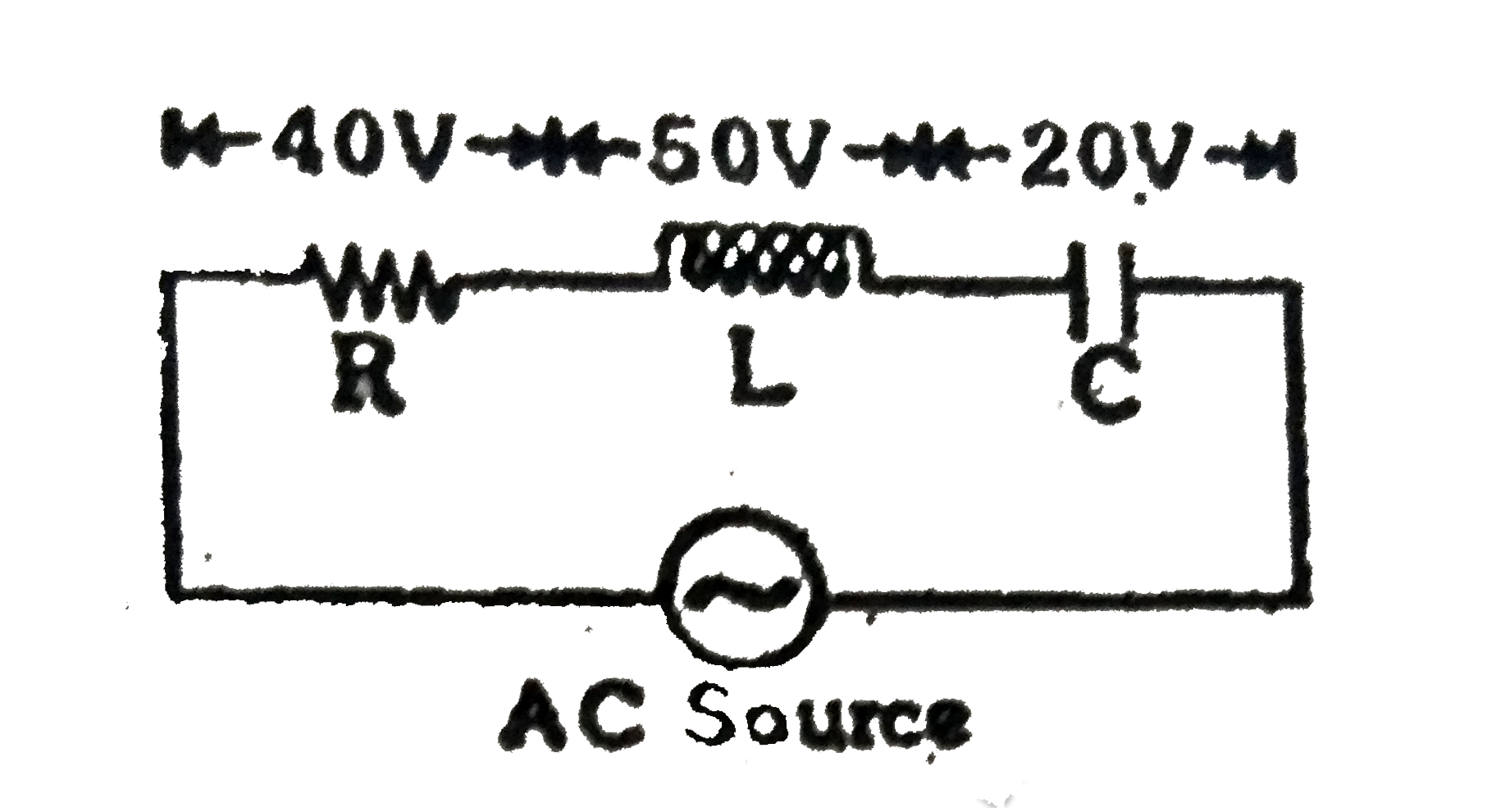
View SolutionIn series LCR circuit, the phase difference between voltage across L and voltage across C is
View Solution