A cubicla room is formed with 6 plane mirrors. An insect moves along the diagonal of the floor with uniform speed. The speed of its image in two adjacent walls is 20√2cm/s.
Then the speed of the image formed on the roof is
20cm/s
40 cm/s
20√2cm/s
10√2cm/s
The correct Answer is:B
To solve the problem step by step, we need to analyze the motion of the insect and how its image is formed in the mirrors of the cubic room.
Step 1: Understand the setup
The insect moves along the diagonal of the floor of a cubic room formed by six plane mirrors. The speed of the insect is uniform, and we denote this speed as V.
Step 2: Analyze the speed of the image in adjacent walls
According to the problem, the speed of the insect's image in two adjacent walls is given as 20√2cm/s. Since the walls are perpendicular to each other, we can denote the speed of the image in one wall as Vx=20√2cm/s and in the adjacent wall as Vy=20√2cm/s.
Step 3: Calculate the resultant speed of the insect
The resultant speed V of the insect can be calculated using the Pythagorean theorem, since the two speeds are perpendicular:
V=√V2x+V2y
Substituting the values:
V=√(20√2)2+(20√2)2
V=√400⋅2+400⋅2
V=√800+800=√1600=40cm/s
Step 4: Determine the speed of the image on the roof
In a cubic room, the speed of the image formed on the roof is equal to the component of the insect's speed that is perpendicular to the mirror surface (the roof). Since the insect is moving along the diagonal of the floor, the speed of the image on the roof will be the same as the resultant speed of the insect.
Thus, the speed of the image formed on the roof is:
Speed of image on roof=V=40cm/s
Final Answer
The speed of the image formed on the roof is 40cm/s.
---
The insect moves along the diagonal of the floor of a cubic room formed by six plane mirrors. The speed of the insect is uniform, and we denote this speed as V.
According to the problem, the speed of the insect's image in two adjacent walls is given as 20√2cm/s. Since the walls are perpendicular to each other, we can denote the speed of the image in one wall as Vx=20√2cm/s and in the adjacent wall as Vy=20√2cm/s.
The resultant speed V of the insect can be calculated using the Pythagorean theorem, since the two speeds are perpendicular:
V=√400⋅2+400⋅2
V=√800+800=√1600=40cm/s
In a cubic room, the speed of the image formed on the roof is equal to the component of the insect's speed that is perpendicular to the mirror surface (the roof). Since the insect is moving along the diagonal of the floor, the speed of the image on the roof will be the same as the resultant speed of the insect.
The speed of the image formed on the roof is 40cm/s.
Similar Questions
A room (cubical) is made of mirros. An insect is moving along the diagonal on the floor such that the velocity of image of insect on two adjacent wall mirrors is 10cmsec. The velocity of image of insect in ceiling mirror is
View SolutionA linear object AB is placed along the axis of a concave mirror. This object is moving towards the mirror with speed U. The speed of the image of the point A is 4U and the speed of the image of B is alSO 4U btu in opposite direction. If the center of the line AB is at a distance L from the mirror then find out the length of the object.
 View Solution
View SolutionUniform speed of 2 cm diameter ball is 20cm/s in a viscous liquid. Then, the speed of 1 cm diameter ball in the same liquid is
View SolutionA plane mirror is placed with its plane at an angle 30∘ with the y-axis. Plane of the mirror is perpendicular to the xy-plane and the length of the mirror is 3m. An insect moves along x-axis starting from a distant point, with speed 2 cm/s. The duration of the time for which the insect can see its shown image in the mirror is:
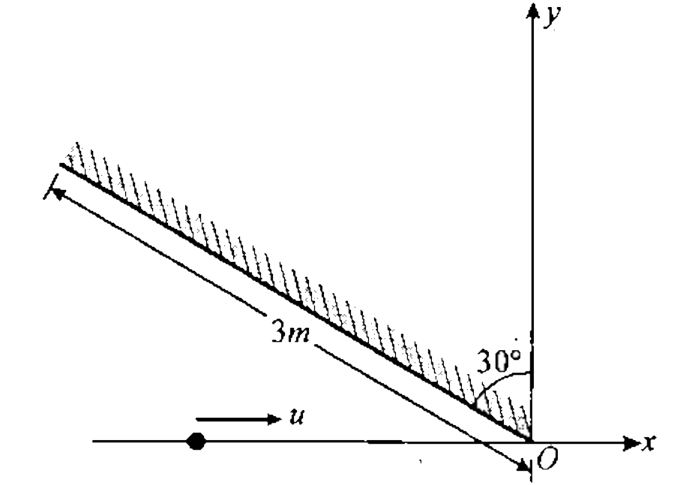 View Solution
View SolutionIn a 3 dimensional space, two particles are moving with uniform speeds of 6m/s and 8m/s along two arbitrary curves. The speed of one particle, as observed by other can be :
View SolutionIn displacement method, convex lens forms a real image of an object for its two different positions. If heights of the images in two cases be 24 cm and 6 cm, then the height of the object is
View SolutionA body of mass 10 kg moving at a height of 2 m, with uniform speed of 2 m/s. Its total energy is
View SolutionAn object is 20 cm away from a concave mirror with focal length 15 cm. If the object moves with a speed of 5 m/s along the axis, then the speed of the image will be
View SolutionAn object is approaching a fixed plane mirror with velocity 3 ms/s at an angle of 45∘ with normal, in a medium of refractive index 4/3. The speed of the image with respect to the mirror is __________m/s.
View SolutionA car is fitted with a convex side-view mirror of focal length 20 cm. A second car 2.8m behind the first car is overtaking the first car at a relative speed of 15 ms. The speed of the image of the second car as seen in the mrror of the first one is:
View Solution

