A room (cubical) is made of mirros. An insect is moving along the diagonal on the floor such that the velocity of image of insect on two adjacent wall mirrors is 10cmsec. The velocity of image of insect in ceiling mirror is
10cms−1
20cms−1
10√2cms−1
10√2cms−1
The correct Answer is:D
To solve the problem, we need to determine the velocity of the image of the insect in the ceiling mirror, given that the velocity of the image on the two adjacent wall mirrors is 10 cm/s.
1. Understanding the Movement of the Insect:
The insect is moving along the diagonal of the floor of a cubical room made of mirrors. This means it has a certain velocity V0 in the diagonal direction.
2. Velocity Components:
Since the insect is moving along the diagonal, we can break its velocity into components. The angle between the diagonal and each wall is 45 degrees. Therefore, the components of the insect's velocity along the two adjacent walls (let's call them wall 1 and wall 2) can be expressed as:
V1=V0cos(45∘)=V0√2
V2=V0cos(45∘)=V0√2
3. Given Information:
We are given that the velocity of the image of the insect on the two adjacent walls is 10 cm/s. Therefore:
V0√2=10 cm/s
4. Finding V0:
To find V0, we can rearrange the equation:
V0=10√2 cm/s
5. Velocity of the Image in the Ceiling Mirror:
The velocity of the image in the ceiling mirror is equal to the actual velocity of the insect, which is V0. Thus:
Vceiling=V0=10√2 cm/s
Final Answer:
The velocity of the image of the insect in the ceiling mirror is 10√2 cm/s.
---
The insect is moving along the diagonal of the floor of a cubical room made of mirrors. This means it has a certain velocity V0 in the diagonal direction.
Since the insect is moving along the diagonal, we can break its velocity into components. The angle between the diagonal and each wall is 45 degrees. Therefore, the components of the insect's velocity along the two adjacent walls (let's call them wall 1 and wall 2) can be expressed as:
V1=V0cos(45∘)=V0√2
V2=V0cos(45∘)=V0√2
We are given that the velocity of the image of the insect on the two adjacent walls is 10 cm/s. Therefore:
V0√2=10 cm/s
To find V0, we can rearrange the equation:
V0=10√2 cm/s
The velocity of the image in the ceiling mirror is equal to the actual velocity of the insect, which is V0. Thus:
Vceiling=V0=10√2 cm/s
The velocity of the image of the insect in the ceiling mirror is 10√2 cm/s.
Similar Questions
A cubicla room is formed with 6 plane mirrors. An insect moves along the diagonal of the floor with uniform speed. The speed of its image in two adjacent walls is 20√2cm/s.
Then the speed of the image formed on the roof is
View SolutionA plane mirror and a person are moving towards each other with same velocity v. Then the velocity of the image is
View SolutionAn object is moving towards a stationary plane mirror with a speed of 2 m/s. Velocity of the image w.r.t. the object is
View SolutionFocal length of the mirror shown in figure is 20cm. Find the image position and its velocity.

View SolutionAn object and a plane mirror are shown in figure. Mirror is moved with velocity V as shown. The velocity of image is :
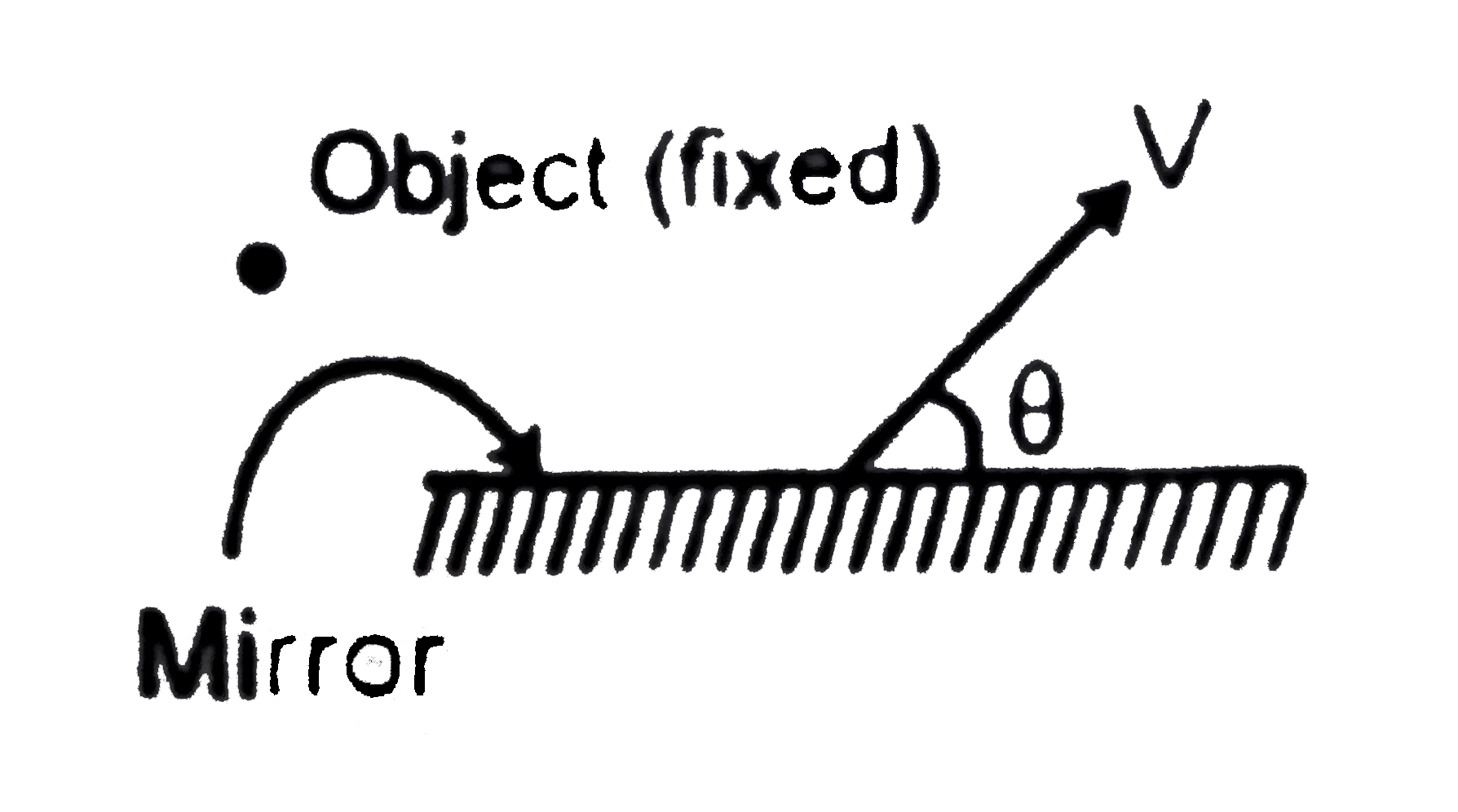 .
.
View SolutionA luminous point object is moving along the principal axis of a concave mirror of focal length 12 cm towards it. When its distance from the mirror is 20 cm its velocity is 4 cm/s. the velocity of the image in cm/s at that instant is
View SolutionFigure shows a plane mirror and an object that are moving towards each other. Find the velocity of image.

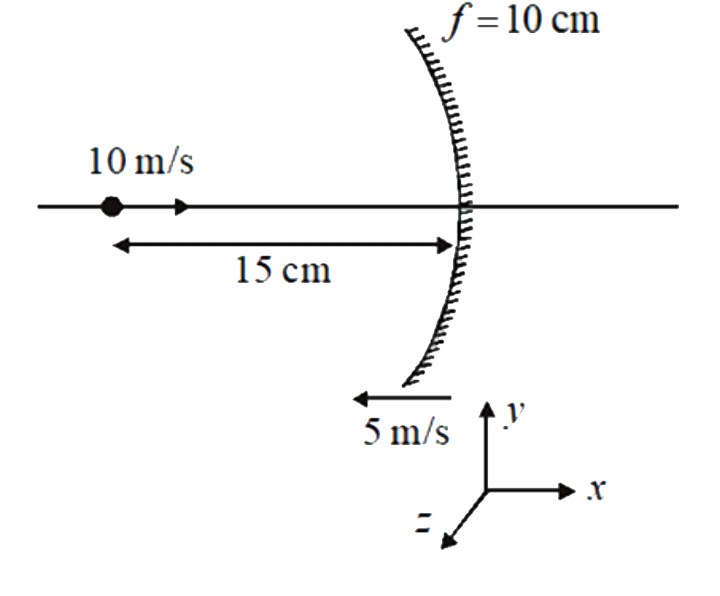
View SolutionAn object and a concave mirror are approaching each other with velocities 10 m/s and 5 m/s as shown in figure. The velocity of image of object at the instant shown in figure is
View SolutionAn insect crawls a distance distance of 4 m along North in 10 s and then a distance of 3 m along East in 5 s. The average velocity of the insect is
View SolutionA point object is moving with a speed v before an arrangement of two mirrors as shown in figure.

Find the velocity of image in mirror M1 with respect to image in mirror M2
View Solution
