In a Young's double slit experiment, films of thickness tA and tB and refcative indices μA and μB are placed in front of slits A and B respectively. If μAtA=μBtB, then the central maxima may
not shift
shift towards A if tA<tB
shift towards B if tA<tB
shift towards A if tA>tB
The correct Answer is:B
To solve the problem, we need to analyze the situation in a Young's double slit experiment with films of different thicknesses and refractive indices placed in front of the slits.
1. Understanding the Setup:
- We have two slits A and B, with films of thickness tA and tB and refractive indices μA and μB placed in front of each slit respectively.
2. Path Difference Calculation:
- The optical path length for light passing through a medium is given by the product of the refractive index and the thickness of the medium.
- For slit A, the optical path length is x1=tAμA.
- For slit B, the optical path length is x2=tBμB.
3. Calculating the Shift:
- The shift due to the films in front of the slits is given by:
x=(tAμA−tBμB)+(tB−tA)
- This can be simplified to:
x=(tAμA−tBμB)+tB−tA
4. Using the Given Condition:
- We are given that μAtA=μBtB.
- This implies that tAμA−tBμB=0.
- Therefore, substituting this into our equation for the shift:
x=0+(tB−tA)=tB−tA
5. Analyzing the Shift:
- If tB=tA, then x=0; the central maxima does not shift.
- If tB>tA, then x>0; the central maxima shifts towards slit A.
- If tB<tA, then x<0; the central maxima shifts towards slit B.
Conclusion:
- The central maxima will not shift if tB=tA.
- The central maxima will shift towards A if tB>tA.
- The central maxima will shift towards B if tB<tA.
Final Answer:
- The correct options are:
- Central maxima does not shift if tB=tA.
- Central maxima shifts towards A if tB>tA.
- Central maxima shifts towards B if tB<tA.
- We have two slits A and B, with films of thickness tA and tB and refractive indices μA and μB placed in front of each slit respectively.
- The optical path length for light passing through a medium is given by the product of the refractive index and the thickness of the medium.
- For slit A, the optical path length is x1=tAμA.
- For slit B, the optical path length is x2=tBμB.
- The shift due to the films in front of the slits is given by:
x=(tAμA−tBμB)+(tB−tA)
- This can be simplified to:
x=(tAμA−tBμB)+tB−tA
- We are given that μAtA=μBtB.
- This implies that tAμA−tBμB=0.
- Therefore, substituting this into our equation for the shift:
x=0+(tB−tA)=tB−tA
- If tB=tA, then x=0; the central maxima does not shift.
- If tB>tA, then x>0; the central maxima shifts towards slit A.
- If tB<tA, then x<0; the central maxima shifts towards slit B.
- The central maxima will not shift if tB=tA.
- The central maxima will shift towards A if tB>tA.
- The central maxima will shift towards B if tB<tA.
- The correct options are:
- Central maxima does not shift if tB=tA.
- Central maxima shifts towards A if tB>tA.
- Central maxima shifts towards B if tB<tA.
Similar Questions
In YDSE, let A and B be two slits. Films of thickness tA and tB and refractive μA and μB are placed in front of A and B, respectively. If μAtA=μAtB, then the central maxima will
View SolutionIn Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
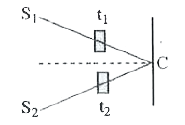
View SolutionIn a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec μ is placed in front of the slit S1, then the path difference (S1P−S2P) is

View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
View Solution(i) In Young's double slit experiment the condition for (a) constructive and (b ) destructive interference at a point on the screen .
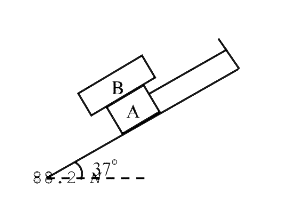
View SolutionFind μs between A and B.
View SolutionIn the Young's double slit experiment , a mica slip of thickness t and refractive index μ is introduced in the ray from first source S1 . By how much distance fringes pattern will be displaced ? (d = distance between the slits and D is the distance between slits and screen)
View SolutionIn the Young's double slit experiment , a mica slip of thickness t and refractive index μ is introduced in the ray from first source S1 . By how much distance fringes pattern will be displaced ? (d = distance between the slits and D is the distance between slits and screen)
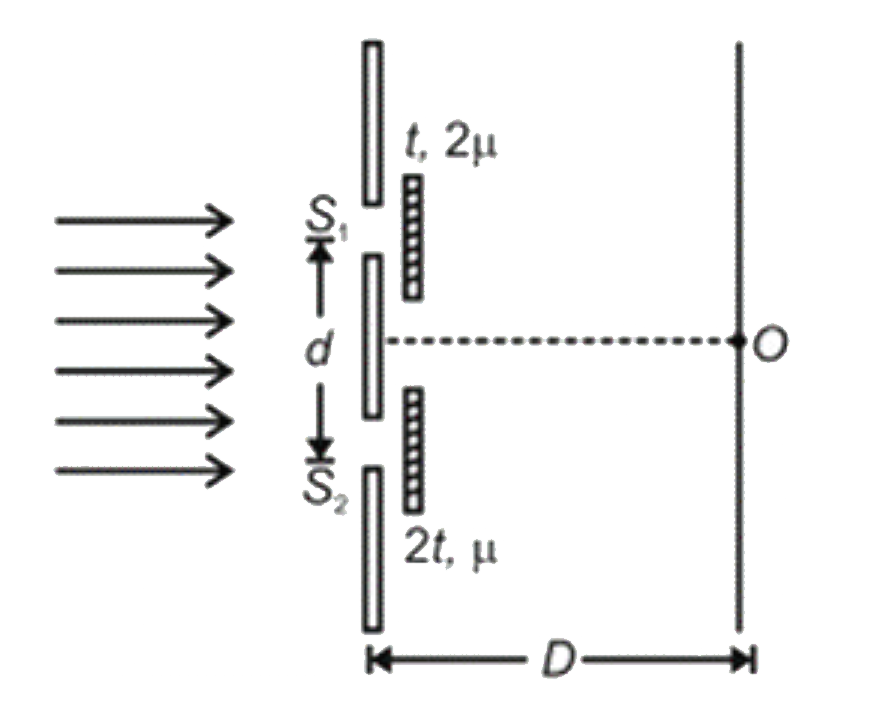
View SolutionIn the YDSE shown the two slits are covered with thin sheets having thickness t & 2t and refractive index 2μ and μ .Find the position (y) of central maxima.

View SolutionIn the YDSE shown below, two slits are covered with thin sheets having a thickness t and 2t and refractive indices 2μ and μ respectively. The position of central maxima is shifted by a distance of N (in cm) from the central position of the screen. Find the value of N.
[d=1mm,D=1m,t=2×10−2mm,μ=32]
View Solution
