In YDSE, let A and B be two slits. Films of thickness tA and tB and refractive μA and μB are placed in front of A and B, respectively. If μAtA=μAtB, then the central maxima will
not shift
shift toward A
shift toward B
(b) if tB<tA and (C ) if tB<tA
The correct Answer is:d
To solve the problem, we need to analyze the situation in the Young's Double Slit Experiment (YDSE) with the introduction of films of different thicknesses and refractive indices in front of the slits.
Step 1: Understand the Phase Change Due to the Films
In YDSE, when light passes through a medium with a refractive index, it experiences a phase change. The phase change (or optical path difference) introduced by a film of thickness t and refractive index μ is given by:
Δx=(μ−1)⋅t
This means that the phase change depends on both the thickness of the film and its refractive index.
Step 2: Calculate the Optical Path Difference
For slits A and B, the optical path differences due to the films can be expressed as:
- For slit A:
ΔxA=(μA−1)⋅tA
- For slit B:
ΔxB=(μB−1)⋅tB
Step 3: Determine the Net Optical Path Difference
The net optical path difference (Δxnet) between the two slits is given by:
Δxnet=ΔxA−ΔxB=(μA−1)⋅tA−(μB−1)⋅tB
Step 4: Use the Given Condition
We are given that:
μA⋅tA=μB⋅tB
From this, we can rearrange to find:
μA⋅tA−μB⋅tB=0
This implies that:
ΔxA=ΔxB
Thus, substituting this into our equation for Δxnet:
Δxnet=(μA−1)⋅tA−(μB−1)⋅tB
Step 5: Analyze the Result
Since we know that μA⋅tA=μB⋅tB, we can conclude that the contributions to the optical path difference from both slits are equal. Therefore:
Δxnet=0
This means that the central maxima will not shift.
Conclusion
The central maxima will not shift.
In YDSE, when light passes through a medium with a refractive index, it experiences a phase change. The phase change (or optical path difference) introduced by a film of thickness t and refractive index μ is given by:
Δx=(μ−1)⋅t
This means that the phase change depends on both the thickness of the film and its refractive index.
For slits A and B, the optical path differences due to the films can be expressed as:
- For slit A:
ΔxA=(μA−1)⋅tA
- For slit B:
ΔxB=(μB−1)⋅tB
The net optical path difference (Δxnet) between the two slits is given by:
Δxnet=ΔxA−ΔxB=(μA−1)⋅tA−(μB−1)⋅tB
We are given that:
μA⋅tA=μB⋅tB
From this, we can rearrange to find:
μA⋅tA−μB⋅tB=0
This implies that:
ΔxA=ΔxB
Thus, substituting this into our equation for Δxnet:
Δxnet=(μA−1)⋅tA−(μB−1)⋅tB
Since we know that μA⋅tA=μB⋅tB, we can conclude that the contributions to the optical path difference from both slits are equal. Therefore:
Δxnet=0
This means that the central maxima will not shift.
The central maxima will not shift.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective11videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
In Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
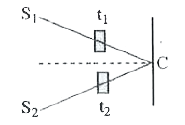 View Solution
View SolutionIn a Young's double slit experiment, films of thickness tA and tB and refcative indices μA and μB are placed in front of slits A and B respectively. If μAtA=μBtB, then the central maxima may
View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
View SolutionLet A and B be two nonsingular square matrices, AT and BT are the tranpose matrices of A and B, respectively, then which of the following are correct ?
View SolutionLet A and B be two nonsingular square matrices, AT and BT are the tranpose matrices of A and B, respectively, then which of the following are coorect ?
View SolutionIf for two gases of molecular weights MA and MB at temperature TA and TB, respectively, TAMB=TBMA, then which property has the same magnitude for both the gases?
View SolutionA system of binary stars of mass mA and mB are moving in circular orbits of radii rA and rB respectively. If TA and TB are at the time periods of masses mA and mB respectively then
View SolutionIn the YDSE shown the two slits are covered with thin sheets having thickness t & 2t and refractive index 2μ and μ .Find the position (y) of central maxima.
 View Solution
View SolutionIn YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
View SolutionIn the YDSE shown below, two slits are covered with thin sheets having a thickness t and 2t and refractive indices 2μ and μ respectively. The position of central maxima is shifted by a distance of N (in cm) from the central position of the screen. Find the value of N.
[d=1mm,D=1m,t=2×10−2mm,μ=32]
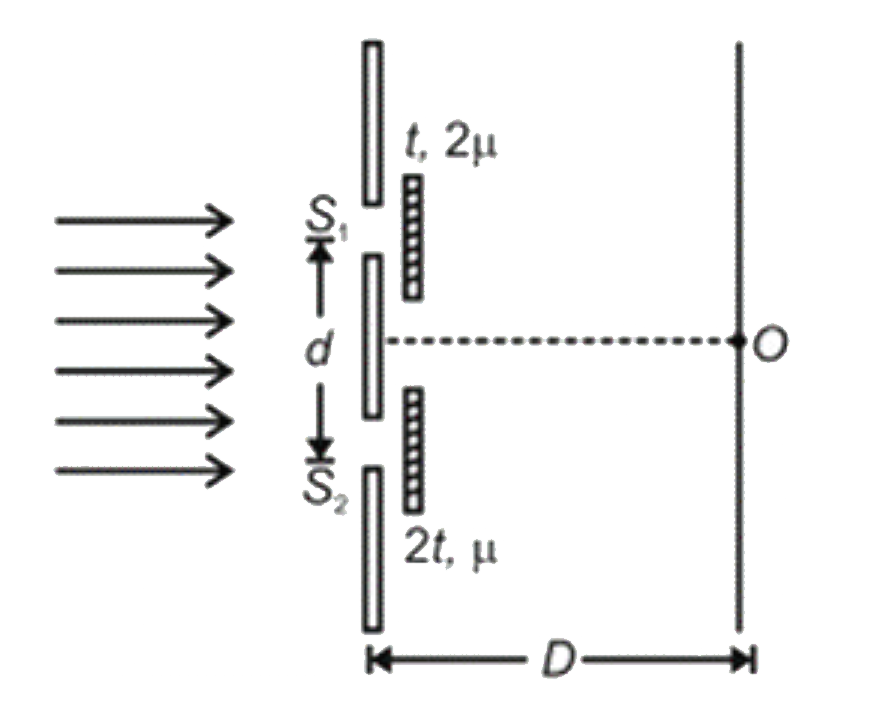 View Solution
View Solution

