A wave front AB moving in air is incident on a plane glass surface. XY , as given in the figure, its position CD after refraction through glass slab is shown along with normal drawn at A and D. the refractive index of glass w.r.t air is given by
sinθsinθ
sinθsinϕ
sinϕsinθ
ABCD
The correct Answer is:A
To find the refractive index of glass with respect to air, we can follow these steps:
1. Identify the Angles:
- Let θ be the angle of incidence (the angle between the incident wave front AB and the normal at point A).
- Let θ′ be the angle of refraction (the angle between the refracted wave front CD and the normal at point D).
2. Use Snell's Law:
- According to Snell's Law, the relationship between the angles of incidence and refraction is given by:
μ=sinθsinθ′
where μ is the refractive index of the medium (glass) with respect to the other medium (air).
3. Determine the Refractive Index:
- The refractive index of glass with respect to air can be expressed as:
μ=VaVg
where Va is the speed of light in air and Vg is the speed of light in glass.
4. Relate the Distances in the Triangles:
- In triangle ABD, the length BD can be expressed as:
BD=AD⋅sinθ
- In triangle ACD, the length AC can be expressed as:
AC=AD⋅sinθ′
5. Substitute the Lengths into the Refractive Index Formula:
- From the triangles, we can write:
BDAC=AD⋅sinθAD⋅sinθ′=sinθsinθ′
- Thus, we can conclude that:
μ=sinθsinθ′
6. Final Answer:
- Therefore, the refractive index of glass with respect to air is:
μ=sinθsinθ′
- Let θ be the angle of incidence (the angle between the incident wave front AB and the normal at point A).
- Let θ′ be the angle of refraction (the angle between the refracted wave front CD and the normal at point D).
- According to Snell's Law, the relationship between the angles of incidence and refraction is given by:
μ=sinθsinθ′
where μ is the refractive index of the medium (glass) with respect to the other medium (air).
- The refractive index of glass with respect to air can be expressed as:
μ=VaVg
where Va is the speed of light in air and Vg is the speed of light in glass.
- In triangle ABD, the length BD can be expressed as:
BD=AD⋅sinθ
- In triangle ACD, the length AC can be expressed as:
AC=AD⋅sinθ′
- From the triangles, we can write:
BDAC=AD⋅sinθAD⋅sinθ′=sinθsinθ′
- Thus, we can conclude that:
μ=sinθsinθ′
- Therefore, the refractive index of glass with respect to air is:
μ=sinθsinθ′
Similar Questions
A certain monochromatic light travelling in air is incident on a glass plate at a polarising angle. Angle of refraction in glass is found to be 32∘ Calculate :
(i) the polarising angle,
(ii) refractive index of glass.
View SolutionA ray of light is incident normally on a plane glass slab. What will be (i) the angle of refraction, and (ii) the angle of deviation for the ray ?
View SolutionUnpolarized light is incident on a plane surface of glass of refractive index μ at angle i. If the reflected light gets totally polarized, write the relation between the angle i and refractive index μ.
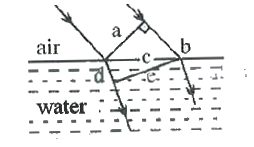
View SolutionFigure shown plane waves refracted for air to water using Huygen.s principle a,b,c,d ,e are lengths on the diagram . The ratio of refractive index of water w.r.t air is
View SolutionA ray of light incident on the horizontal surface of a glass slab at 70∘ just grazes the adjacent vertical surface after refraction. Complete the critical angle and refractive index of glass.
View SolutionA trianglular prims of glass is shown in the figure. A ray incident normally to one face is totally reflected. If θ=45∘ the refractive index of glass is

View SolutionUnpolarized light is incident on a plane glass surface having refractive index . The angle of incidence at which reflected and refracted rays would become perpendicular to each other is :
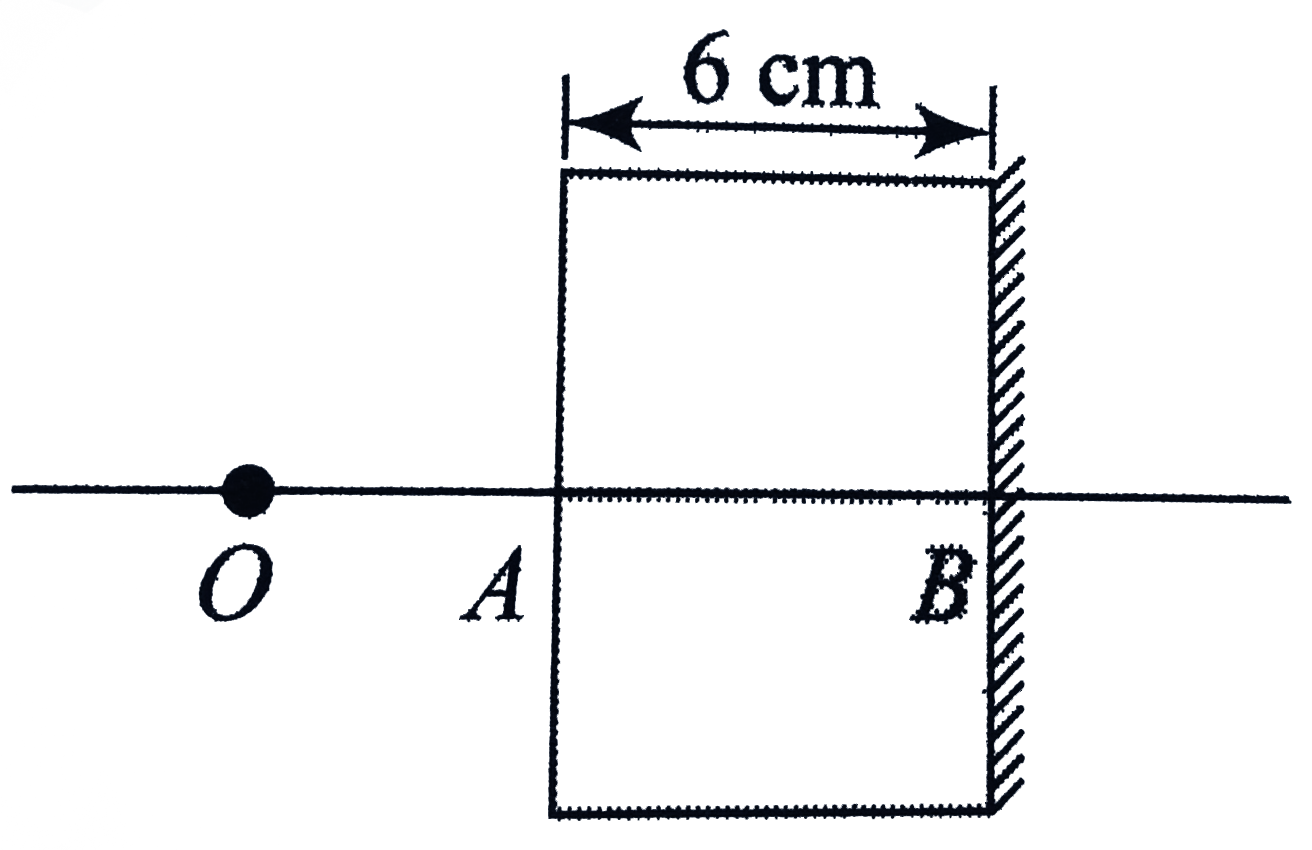
View SolutionAn object O is placed at 8cm in front of a glass slab, whose one face is silvered as shown in Figure. The thickness of the slab is 6cm. If the image formed 10 cm behind the silvered face, find the refractive index of glass.
View SolutionA ray LM of monochromatic light incident normally on one refracting surface AB of a regular glass prism ABC emerges in air from the adjacent surface C as shown in figure. Calculate the refractive index of the material of the prism.
View SolutionThe refractive index of water with respect to air is aμw and of glass with respect to air is aμg. Express the refractive index of glass with respect to water.
View Solution
