A resistor and inductor are connected in series through a battery.
The switch is closed at time t=0 . Then what is the magnitude of current flowing when rate of increases of magnetic energy in the inductor is maximum
I=VR
I=V2R
I=V4R
I=VRin2
The correct Answer is:B
To solve the problem step by step, we need to analyze the circuit consisting of a resistor (R) and an inductor (L) connected in series with a battery (V). We want to find the magnitude of the current flowing when the rate of increase of magnetic energy in the inductor is maximum.
Step 1: Understand the Circuit
When the switch is closed at time t=0, the current I(t) in the circuit increases over time according to the formula:
I(t)=VR(1−e−RLt)
where V is the voltage of the battery, R is the resistance, and L is the inductance.
Step 2: Magnetic Energy in the Inductor
The magnetic energy U stored in the inductor at any time t is given by:
U=12LI2
Step 3: Rate of Change of Magnetic Energy
To find the rate of change of magnetic energy, we differentiate U with respect to time t:
dUdt=LIdIdt
Step 4: Find dIdt
The derivative of the current I(t) with respect to time t is:
dIdt=VR⋅RLe−RLt=VLe−RLt
Step 5: Substitute dIdt into dUdt
Substituting dIdt into the expression for dUdt:
dUdt=LI(VLe−RLt)=VIe−RLt
Step 6: Find Maximum Rate of Change
To find when dUdt is maximum, we need to express I in terms of e−RLt:
I=VR(1−e−RLt)
Substituting this into dUdt:
dUdt=V(VR(1−e−RLt))e−RLt
=V2R(1−e−RLt)e−RLt
Step 7: Find the Condition for Maximum
To maximize dUdt, we set the derivative of dUdt with respect to t to zero. After simplification, we find that the maximum occurs when:
I=V2R
Conclusion
Thus, the magnitude of the current flowing when the rate of increase of magnetic energy in the inductor is maximum is:
V2R
When the switch is closed at time t=0, the current I(t) in the circuit increases over time according to the formula:
I(t)=VR(1−e−RLt)
where V is the voltage of the battery, R is the resistance, and L is the inductance.
The magnetic energy U stored in the inductor at any time t is given by:
U=12LI2
To find the rate of change of magnetic energy, we differentiate U with respect to time t:
dUdt=LIdIdt
The derivative of the current I(t) with respect to time t is:
dIdt=VR⋅RLe−RLt=VLe−RLt
Substituting dIdt into the expression for dUdt:
dUdt=LI(VLe−RLt)=VIe−RLt
To find when dUdt is maximum, we need to express I in terms of e−RLt:
I=VR(1−e−RLt)
Substituting this into dUdt:
dUdt=V(VR(1−e−RLt))e−RLt
=V2R(1−e−RLt)e−RLt
To maximize dUdt, we set the derivative of dUdt with respect to t to zero. After simplification, we find that the maximum occurs when:
I=V2R
Thus, the magnitude of the current flowing when the rate of increase of magnetic energy in the inductor is maximum is:
V2R
Similar Questions
Two inductors are connected in parallel and switch S is closed at t=0
 View Solution
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
 View Solution
View SolutionAn inductor of 2 H and a resistance of 10Ω are connects in series with a battery of 5 V. The initial rate of change of current is
View SolutionA charged capacitro and an inductor are connected in series. At time t = 0 , the current is zero but the capacitor is charged, If T is the period of resulting oscillations, then the time after which current in the circuit becomes maximum , is
View Solutionthere in no current part of this circuit for time t<o. Switch S is closed at t=0.

The rate at which the current through the inductor increases initially isView SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
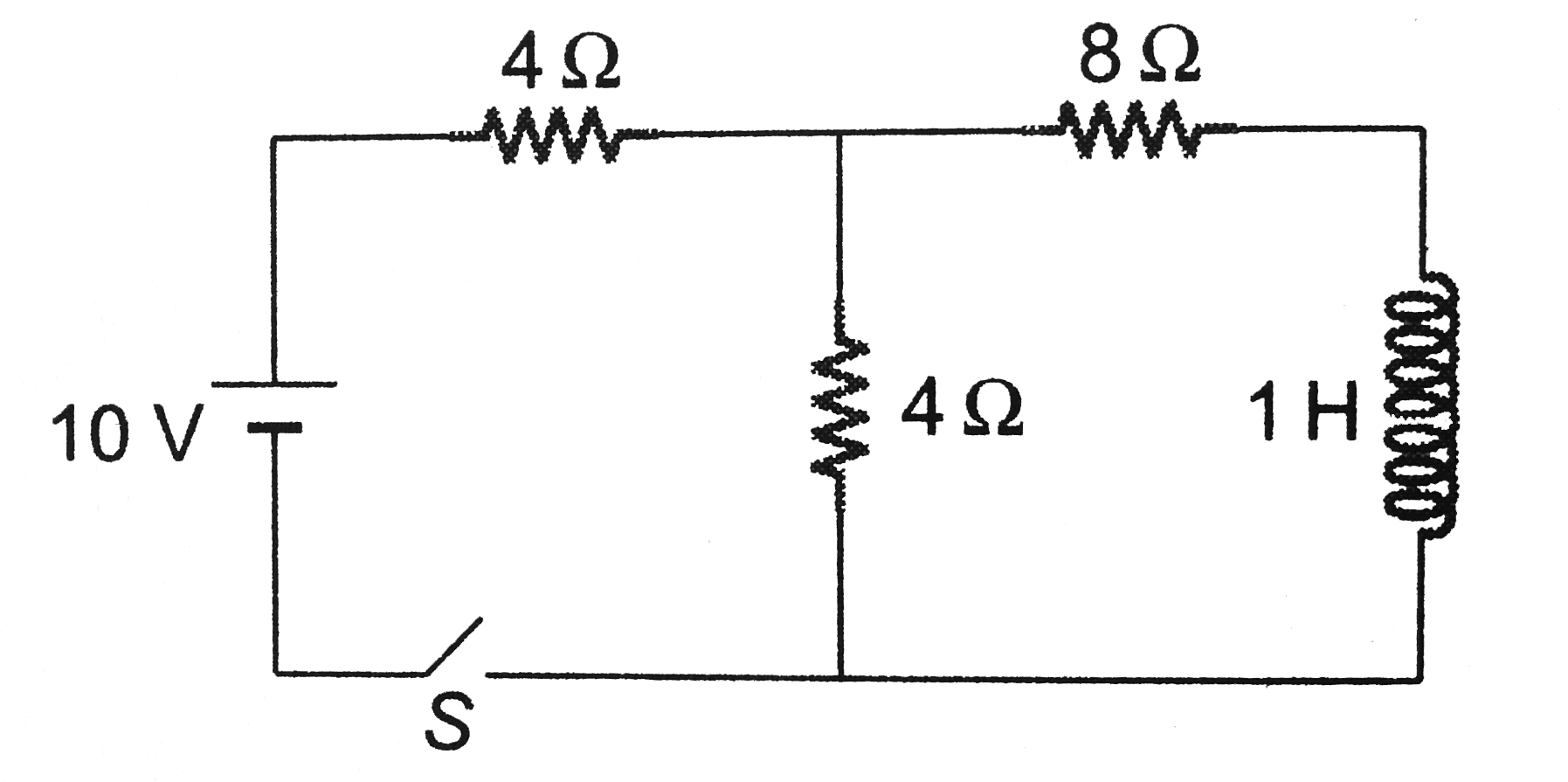 View Solution
View SolutionA solenoid L and a resistor R are connected in series to a battery, through a switch. When the switch is put on, current I flowing through it varies with time t as shown in which of the graphs given below :∗
View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.
 View Solution
View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.
 View Solution
View SolutionA capacitor is charged to a potential of V0. It is connected with an inductor through a switch S. The switch is closed at time t=0. Which of the following statement(s) is/are correct?
 View Solution
View Solution

