A charged capacitro and an inductor are connected in series. At time t = 0 , the current is zero but the capacitor is charged, If T is the period of resulting oscillations, then the time after which current in the circuit becomes maximum , is
T
T4
T2
T6
The correct Answer is:B
To solve the problem, we need to analyze the behavior of a series LC circuit consisting of a charged capacitor and an inductor. The key points to consider are the energy oscillation between the capacitor and the inductor and the relationship between time and current in this oscillating system.
1. Understanding Initial Conditions:
- At time t=0, the capacitor is fully charged, and the current in the circuit is zero. This means all the energy is stored in the capacitor as electric potential energy.
2. Energy in the Capacitor:
- The energy stored in the capacitor at this moment can be expressed as:
UC=Q22C
where Q is the charge on the capacitor and C is the capacitance.
3. Oscillation in the LC Circuit:
- The energy in the circuit oscillates between the capacitor and the inductor. As the capacitor discharges, the current starts to flow through the inductor, and energy is transferred to the inductor as magnetic energy.
4. Current and Maximum Energy Transfer:
- The current in the circuit reaches its maximum value when all the energy has been transferred from the capacitor to the inductor. This occurs after a quarter of the oscillation period, T/4.
5. Period of Oscillation:
- The period T of the oscillation in an LC circuit is given by:
T=2π√LC
where L is the inductance.
6. Time for Maximum Current:
- Since the current is zero at t=0 and reaches its maximum at t=T/4, we conclude that the time after which the current in the circuit becomes maximum is:
t=T4
Final Answer:
The time after which the current in the circuit becomes maximum is T4.
---
- At time t=0, the capacitor is fully charged, and the current in the circuit is zero. This means all the energy is stored in the capacitor as electric potential energy.
- The energy stored in the capacitor at this moment can be expressed as:
UC=Q22C
where Q is the charge on the capacitor and C is the capacitance.
- The energy in the circuit oscillates between the capacitor and the inductor. As the capacitor discharges, the current starts to flow through the inductor, and energy is transferred to the inductor as magnetic energy.
- The current in the circuit reaches its maximum value when all the energy has been transferred from the capacitor to the inductor. This occurs after a quarter of the oscillation period, T/4.
- The period T of the oscillation in an LC circuit is given by:
T=2π√LC
where L is the inductance.
- Since the current is zero at t=0 and reaches its maximum at t=T/4, we conclude that the time after which the current in the circuit becomes maximum is:
t=T4
The time after which the current in the circuit becomes maximum is T4.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - B) (Objective Type Questions (One option is correct))
14 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - C ) (Objective Type Questions) ( More than one option are correct)
2 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Try Yourself
15 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
If maximum energy is stored in capacitor at t = 0 then find the time after which current in the circuit will be maximum.
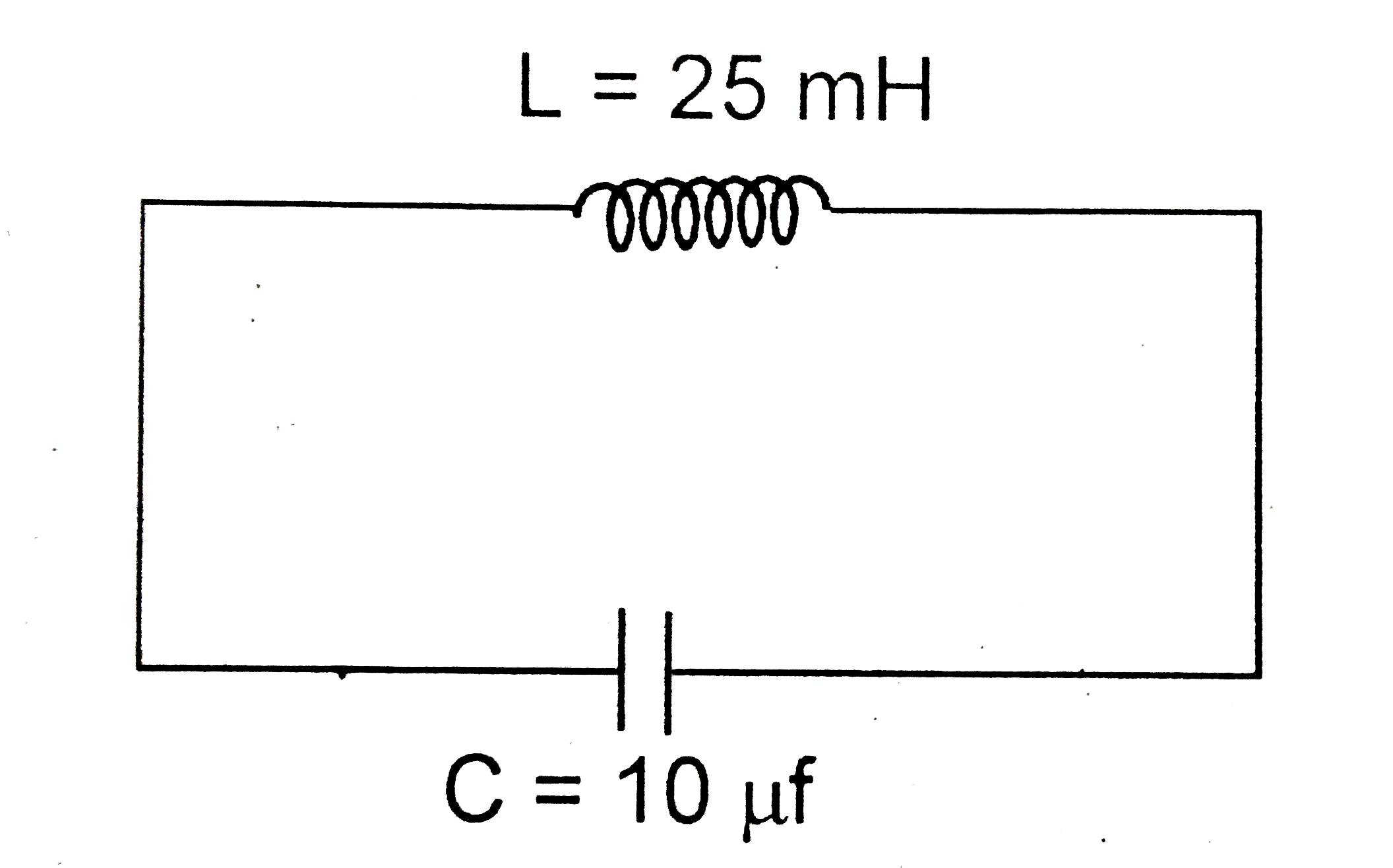
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t

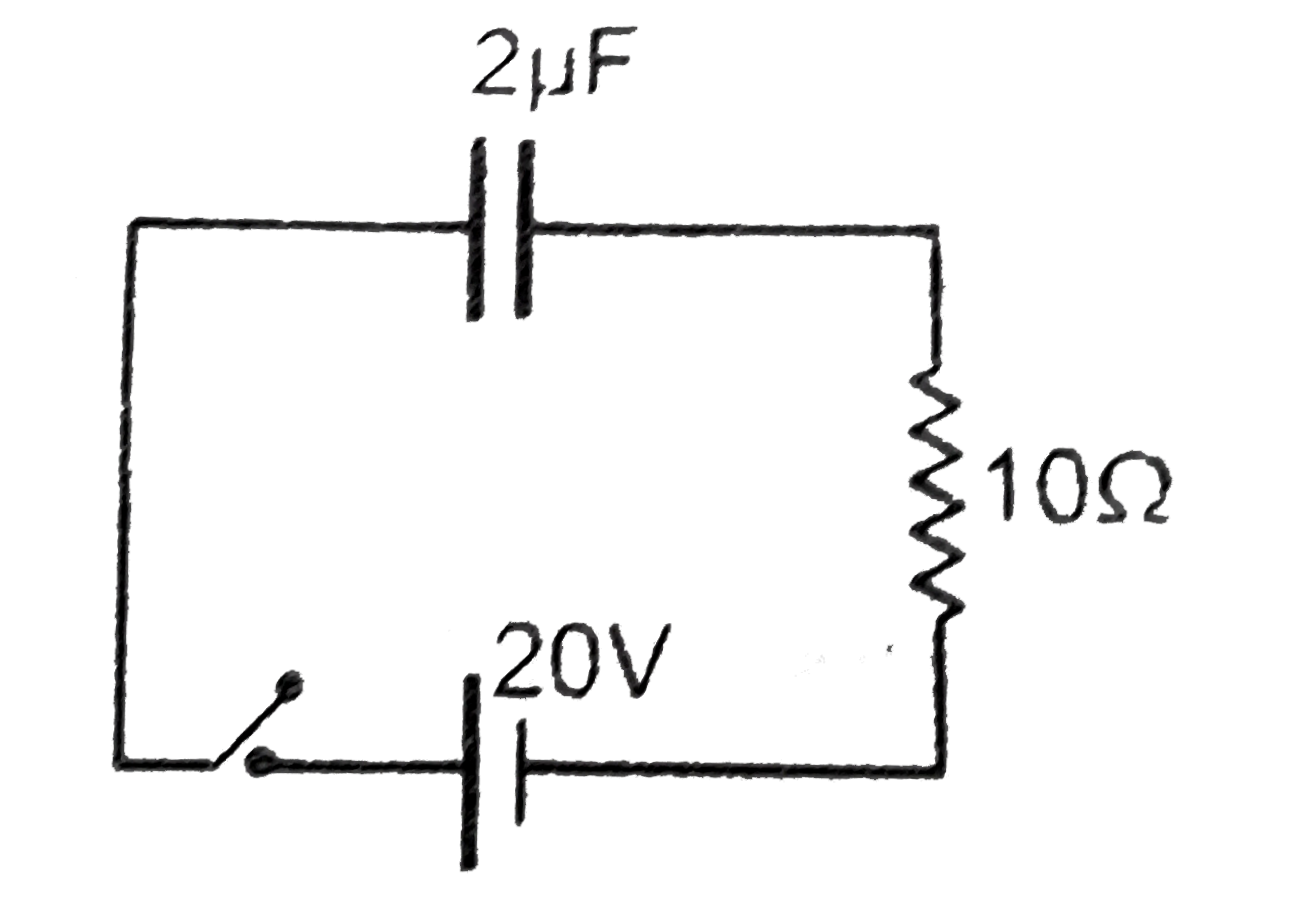
View SolutionInitially capacitor is uncharged at t=0 switch is closed. Charge on capacitor when current in the circuit is 10% of maximum current :
View SolutionThe potential difference across a 2-H inductor as a function of time is shown in Fig. At time t = 0, current is zero.
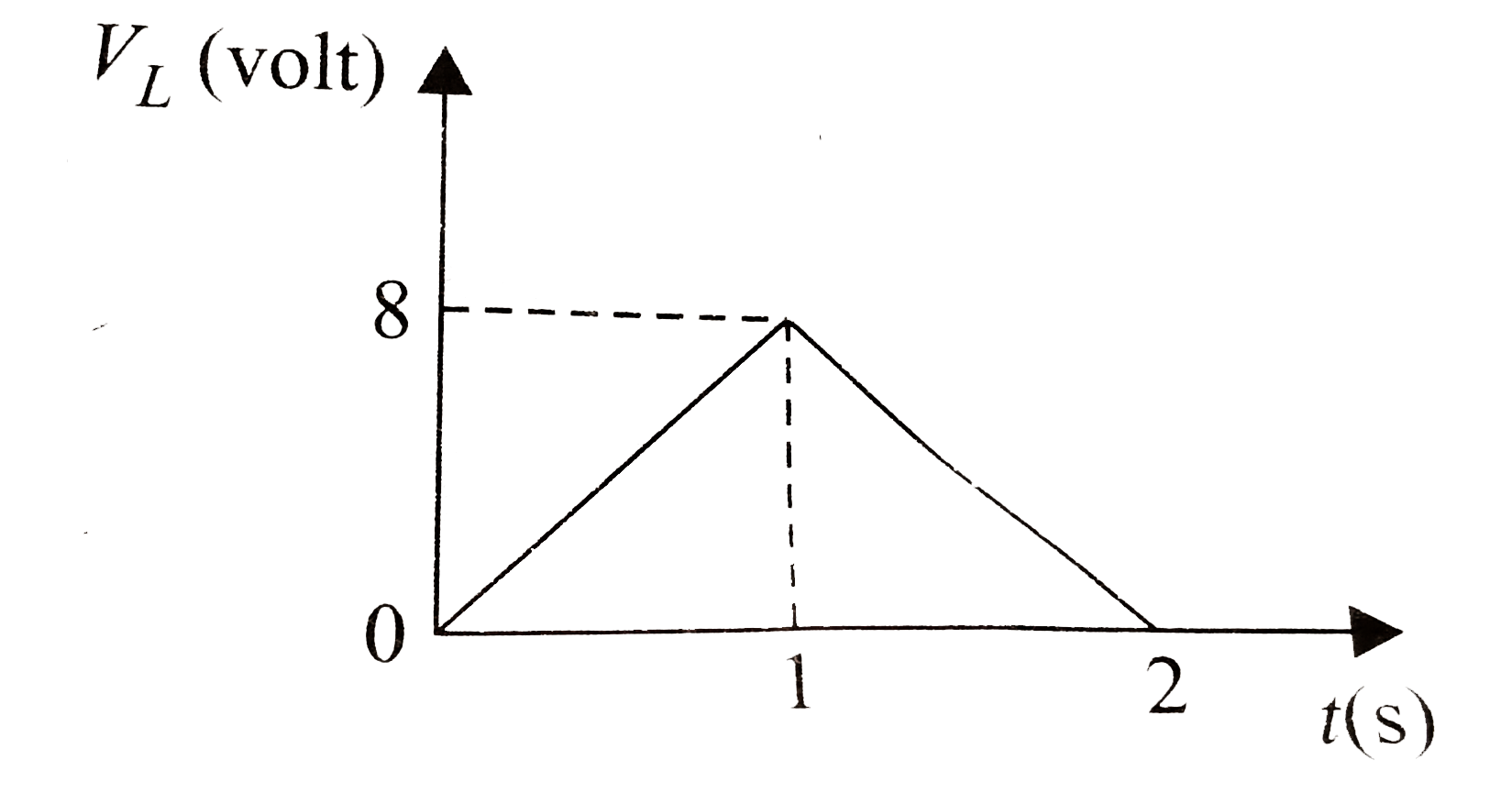
Current at t = 1 s is
View SolutionAn an ideal parallel LC circuit, the capacitor is charged by connecting it to a DC source which is then disconnected. The current in the circuit
View SolutionThe potential difference across a 2H inductor as a function of time is shown in figure. At time t=0, current is zero
Current t=2 second is
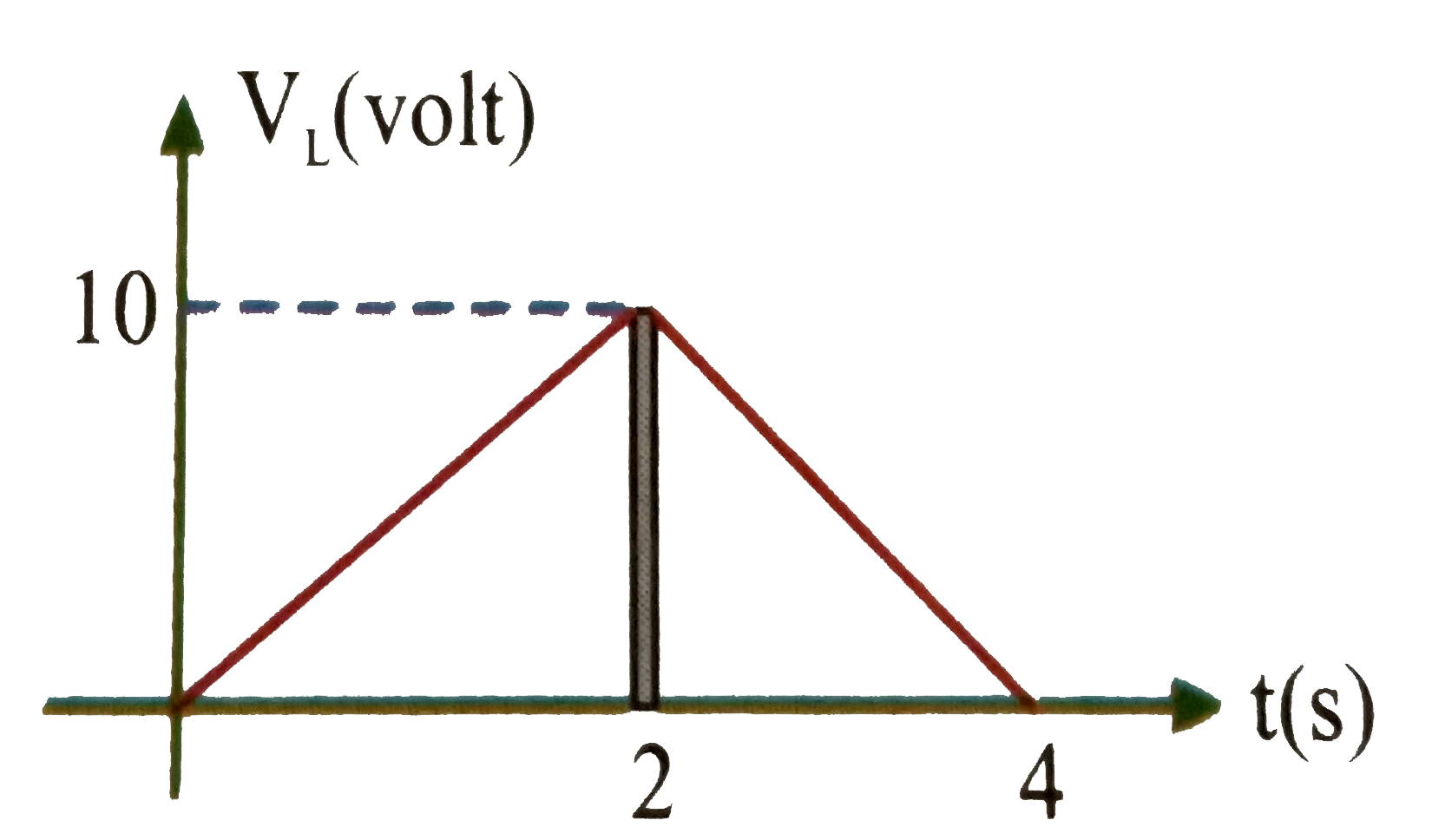
View SolutionA resistor and inductor are connected in series through a battery.
The switch is closed at time t=0 . Then what is the magnitude of current flowing when rate of increases of magnetic energy in the inductor is maximum
View SolutionThe conduction current in ideal case through a circuit is zero when charge on capacitor is
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionThe potential difference across a 2-H inductor as a function of time is shown in Fig. At time t = 0, current is zero.
The variation of current versus time is
View Solution