Gravitational potential at point 'P' due to triangular plate is V0 . Find the gravitational potential due to the given plate at point 'Q' as shown in figure. (both plates are made by same meterial)
V0
2V0
4V0
3V0
The correct Answer is:A
To find the gravitational potential at point 'Q' due to the triangular plate, we can follow these steps:
1. Understand the Given Information:
- The gravitational potential at point 'P' due to the triangular plate is given as V0.
- The triangular plate has sides of length A.
- The distance from point 'Q' to the triangular plate is also A.
2. Determine the Geometry:
- The distance from point 'P' to the center of mass of the triangular plate is A.
- The distance from point 'Q' to the center of mass of the triangular plate is 2A (since it is at a distance of A from the plate and the plate's height is also A).
3. Use the Formula for Gravitational Potential:
- The gravitational potential V due to a mass M at a distance r is given by:
V∝Mr
- Since the mass M of the triangular plate is constant, we can express the potentials at points 'P' and 'Q' in terms of their distances from the plate.
4. Relate the Potentials:
- At point 'P', the potential is:
VP∝MA
- At point 'Q', the potential is:
VQ∝M2A
5. Express VQ in Terms of V0:
- Since V0 is defined as the potential at point 'P':
V0∝MA
- Therefore, we can express VQ as:
VQ∝M2A=12⋅MA=12V0
6. Final Expression:
- Thus, the gravitational potential at point 'Q' can be expressed as:
VQ=12V0
Conclusion:
The gravitational potential at point 'Q' is 12V0.
- The gravitational potential at point 'P' due to the triangular plate is given as V0.
- The triangular plate has sides of length A.
- The distance from point 'Q' to the triangular plate is also A.
- The distance from point 'P' to the center of mass of the triangular plate is A.
- The distance from point 'Q' to the center of mass of the triangular plate is 2A (since it is at a distance of A from the plate and the plate's height is also A).
- The gravitational potential V due to a mass M at a distance r is given by:
V∝Mr
- Since the mass M of the triangular plate is constant, we can express the potentials at points 'P' and 'Q' in terms of their distances from the plate.
- At point 'P', the potential is:
VP∝MA
- At point 'Q', the potential is:
VQ∝M2A
- Since V0 is defined as the potential at point 'P':
V0∝MA
- Therefore, we can express VQ as:
VQ∝M2A=12⋅MA=12V0
- Thus, the gravitational potential at point 'Q' can be expressed as:
VQ=12V0
The gravitational potential at point 'Q' is 12V0.
Similar Questions
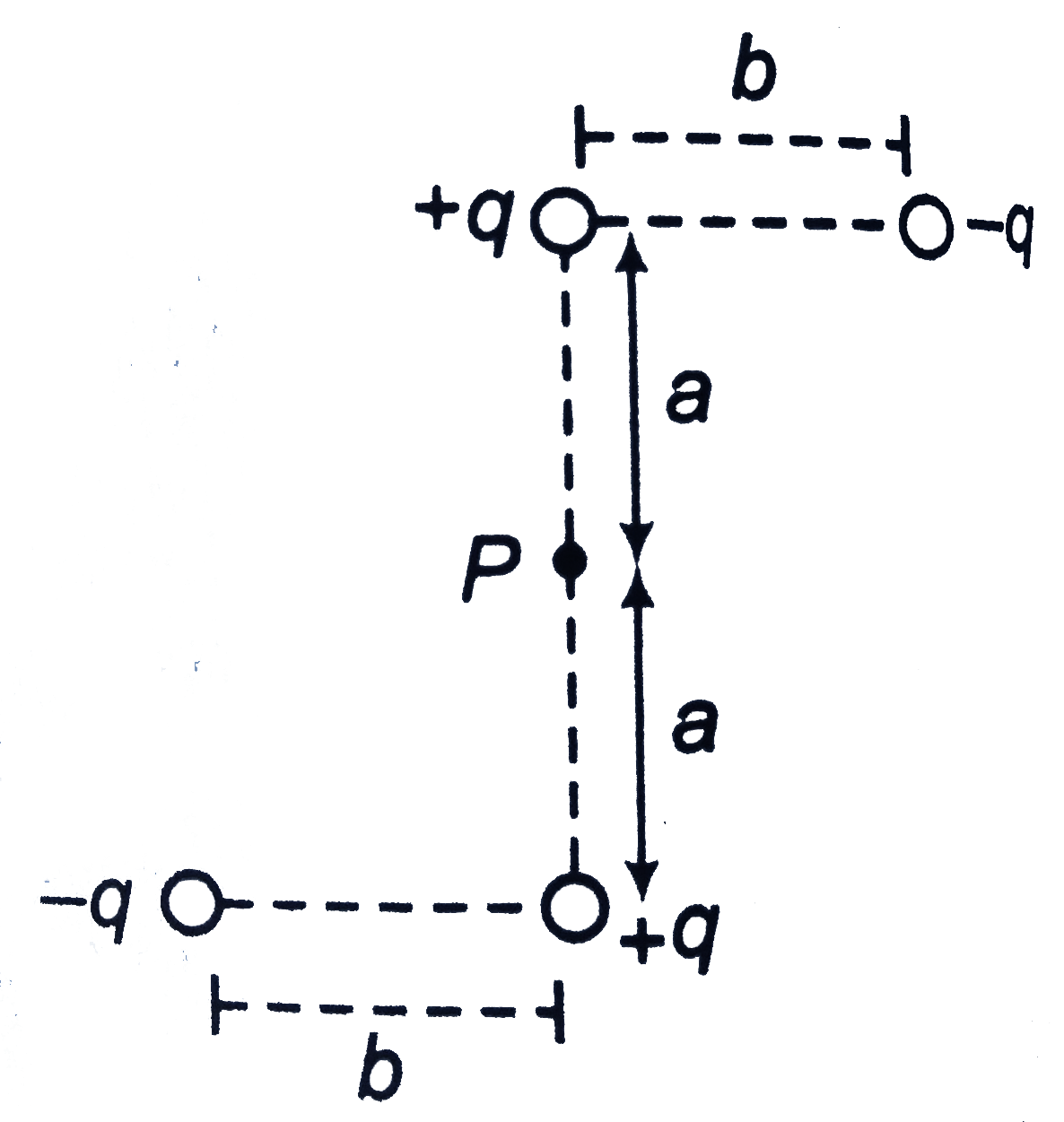
The electrostatic potential due to the charge configuration at point P as shown in figure for b << a is
View SolutionThe gravitational potential due to a mass distribution is V=A√x2+a2. Find the gravitational field.
View SolutionThe gravitational potential due to a mass distribution is V=3X2Y+Y3Z. Find the gravitational filed.
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. It is possile to have
View SolutionGravitational potential at a distance 'r' from a point mass 'm' is
V=−GMr
Find gravitational field strength at that point.
View SolutionOn the surface of earth acceleration due to gravity is g and gravitational potential is V. Match the following.

View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View SolutionAssertion : If gravitational potential at some point is zero, then gravitational field strength at that point will also be zero.
Reason : Except at infinity gravitational potential due to a system of point masses at some finite distance can't be zero.
View SolutionThe gravitational potential due to a mass distrubution is given by V=8xx2+p2. Find gravitational field at x = p.
View SolutionThe gravitational potential due to earth at infinite distance from it is zero. Let the gravitational potential at a point P be −5Jkg−1. Suppose, we arbitrarily assume the gravitational potential at infinity to be +10Jkg−1, then the gravitational potential at P will be
View Solution
