The area of F.t curve is A. If one of the colliding bodies of mass m is at rest, find its speed just after the collision.
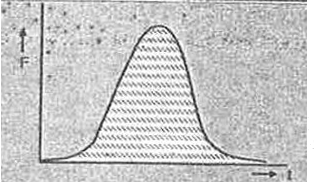
The area of F-t curve gives the impulse of the force F during the time. That is equal to the change in momentum of the colliding bodies. Since one of the colliding body was at rest just before the collision, the change in its momentum during the impacxt is equal to momentum just after the impact, that is mv.
⇒∫Fdt=mv
Since ∫Fdt=A
⇒v=A/m.
Similar Questions
Orbital velocity of a satellite in its orbit (around earth) of radius r is v. It collides with another body in its orbit and comes to rest just after the collision. Taking the radius of earth as R, the speed with which it will fall on the surface of earth will be :
View SolutionA particle A of mass m initially at rest slides down a height of 1.25 m on a frictionless ramp, collides with and sticks to an identical particles B of mass m at rest as shown in the figure.

Then, particles A and B together collide elastically with particle G of mass 2m at rest. The speed of particle G after the collision with combined body (A+B) would be (Take, g=10ms−2)View Solution
Knowledge Check
- Question 1 - Select One
Two objects, one of mass 3 kg and moving with speed of 2 m/s and the other of mass 5 kg and speed 2 m/s, move toward each other and collide head-on. If the collision is perfectly inelastic, find the speed of the object after the collision.
A0.25m/sB0.5m/sC0.75m/sD1m/s
A glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View SolutionA particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
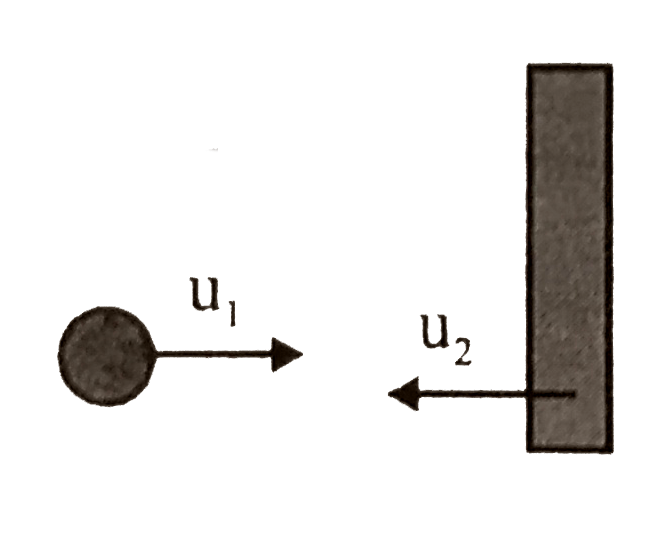 View Solution
View SolutionA small uniform solid sphere A rolls down a fixed surface starting at a height h and collides elastically with a sphere B which is identical in size to A but has twice its mass. The speed of the sphere B, just after the collision is
 View Solution
View SolutionBody A of mass 4m moving with speed u collides with another body B of mass 2m at rest the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
View Solution

