A block A of mass m is lying on a rough horizontal surface. Another block B of mass 2m having velocity 10 m/s just before collision, makes head on collision with stationary block A. The coefficient of restitution between blocks is 0.5, and the coefficient of friction between blocks and ground is 0.3. Find the distance between the blocks when they stop.
The correct Answer is:12.5 m
To solve the problem step by step, we need to analyze the situation involving two blocks, A and B, during and after their collision. Here's the detailed solution:
Step 1: Understand the initial conditions
- Block A (mass = m) is stationary.
- Block B (mass = 2m) is moving with a velocity of 10 m/s before the collision.
- Coefficient of restitution (e) = 0.5.
- Coefficient of friction (μ) = 0.3.
Step 2: Apply conservation of momentum
Before the collision, the total momentum of the system is:
Initial momentum=(2m⋅10)+(m⋅0)=20m
After the collision, let the velocities of blocks A and B be v1 and v2 respectively. The total momentum after the collision is:
Final momentum=mv1+2mv2
Setting the initial momentum equal to the final momentum:
20m=mv1+2mv2
Dividing through by m:
20=v1+2v2(Equation 1)
Step 3: Apply the coefficient of restitution
The coefficient of restitution relates the velocities before and after the collision:
e=v1−v210−0
Substituting the value of e:
0.5=v1−v210
Multiplying through by 10:
v1−v2=5(Equation 2)
Step 4: Solve the equations simultaneously
We have two equations:
1. 20=v1+2v2
2. v1−v2=5
From Equation 2, we can express v1 in terms of v2:
v1=v2+5
Substituting this into Equation 1:
20=(v2+5)+2v2
Simplifying:
20=3v2+5
15=3v2
v2=5m/s
Now substituting v2 back to find v1:
v1=5+5=10m/s
Step 5: Determine the deceleration due to friction
The frictional force acting on each block is given by:
f=μ⋅m⋅g
Where g≈10m/s2. Thus, for block A (mass = m):
fA=0.3⋅m⋅10=3m
And for block B (mass = 2m):
fB=0.3⋅2m⋅10=6m
The deceleration (a) for both blocks due to friction is:
a=fm=3mm=3m/s2(for A)
a=6m2m=3m/s2(for B)
Step 6: Calculate the stopping distances
Using the equation of motion:
v2=u2+2as
Where v=0 (final velocity), u is the initial velocity, a is the deceleration, and s is the distance traveled.
For block A (initial velocity u1=10m/s):
0=(10)2−2⋅3⋅s1
100=6s1⟹s1=1006≈16.67m
For block B (initial velocity u2=5m/s):
0=(5)2−2⋅3⋅s2
25=6s2⟹s2=256≈4.17m
Step 7: Find the distance between the blocks when they stop
The distance x between the two blocks when they stop is:
x=s1−s2=16.67−4.17≈12.5m
Final Answer
The distance between the blocks when they stop is approximately 12.5 meters.
---
- Block A (mass = m) is stationary.
- Block B (mass = 2m) is moving with a velocity of 10 m/s before the collision.
- Coefficient of restitution (e) = 0.5.
- Coefficient of friction (μ) = 0.3.
Before the collision, the total momentum of the system is:
Initial momentum=(2m⋅10)+(m⋅0)=20m
After the collision, let the velocities of blocks A and B be v1 and v2 respectively. The total momentum after the collision is:
Final momentum=mv1+2mv2
Setting the initial momentum equal to the final momentum:
20m=mv1+2mv2
Dividing through by m:
20=v1+2v2(Equation 1)
The coefficient of restitution relates the velocities before and after the collision:
e=v1−v210−0
Substituting the value of e:
0.5=v1−v210
Multiplying through by 10:
v1−v2=5(Equation 2)
We have two equations:
1. 20=v1+2v2
2. v1−v2=5
v1=v2+5
Substituting this into Equation 1:
20=(v2+5)+2v2
Simplifying:
20=3v2+5
15=3v2
v2=5m/s
Now substituting v2 back to find v1:
v1=5+5=10m/s
The frictional force acting on each block is given by:
f=μ⋅m⋅g
Where g≈10m/s2. Thus, for block A (mass = m):
fA=0.3⋅m⋅10=3m
And for block B (mass = 2m):
fB=0.3⋅2m⋅10=6m
The deceleration (a) for both blocks due to friction is:
a=fm=3mm=3m/s2(for A)
a=6m2m=3m/s2(for B)
Using the equation of motion:
v2=u2+2as
Where v=0 (final velocity), u is the initial velocity, a is the deceleration, and s is the distance traveled.
0=(10)2−2⋅3⋅s1
100=6s1⟹s1=1006≈16.67m
0=(5)2−2⋅3⋅s2
25=6s2⟹s2=256≈4.17m
The distance x between the two blocks when they stop is:
x=s1−s2=16.67−4.17≈12.5m
The distance between the blocks when they stop is approximately 12.5 meters.
Similar Questions
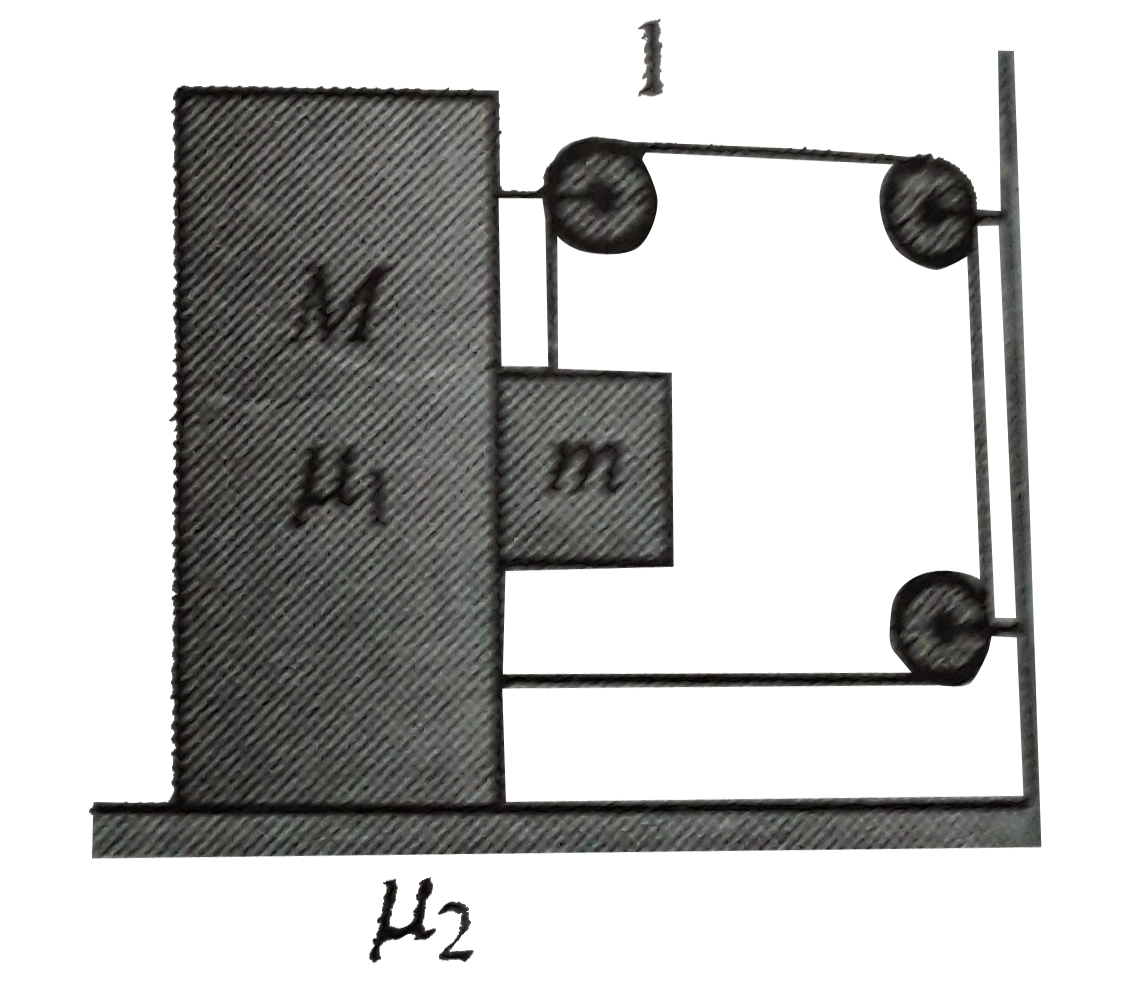
The block of mass M and are arrenged as the situation in fig is shown.The coefficient of friction between two block is μand that between the bigger block and the ground is μ find the acceleration of the block .
View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View SolutionA block A of mass 2 kg rests on a horizontal surface. Another block B of mass 1 kg moving at a speed of m/s when at a distance of 16 cm from A. collides elastically with A. The coefficeint of friction between the horizontal surface and earth of the blocks is 0.2. Then (g=10m/s2)
View SolutionA long block A of mass M is at rest on a smooth horizontal surface.A small block B of mass M/2 is placed on A at one end and projected along A with some veklocity v.The coefficient of friction between the block is μ then , the accelerations of blocks A and B before reaching a common velocity will be respectively

View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionBlock A has a mass 3kg and is sliding on a rough horizontal surface with a velocity uA=2m/s when it makes a direct collision with block B, which has a mass of 2kg and is originally at rest. The collision is perfectly elastic. Determine the velocity of each block just after collision and the distance between the blocks when they stop sliding. The coefficient of kinetic friction between the blocks and the plane is μk=0.3 ( Take g=10m/s2)
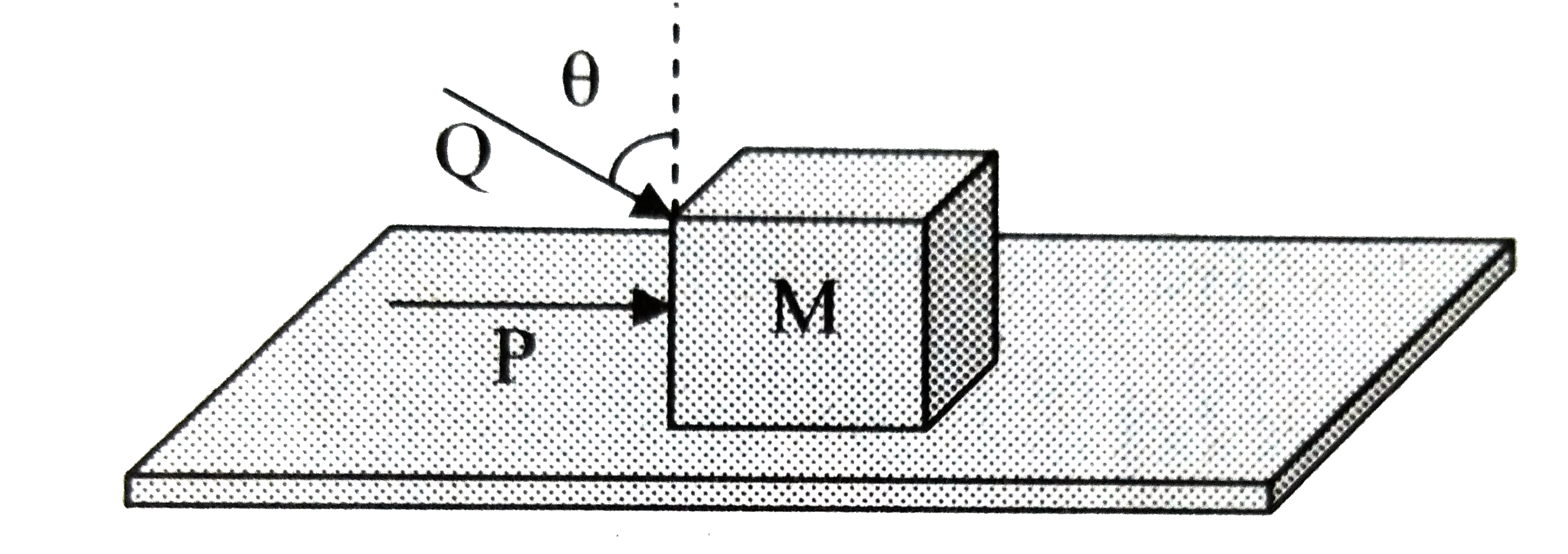
View SolutionA block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and g=10ms−2 The frictional force on the block is
View SolutionA block of mass m is kept over another block of mass 2 m and the system rests on a smooth horizontal surface. The coefficient of friction between the blocks is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system, when a force mg is applied to the lower block.
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View Solution
