Two skaters A & B of mass M and 2M are standing together on a frictionless ice surface. They push each other apart. The skater B moves away from A with a speed of 2 m/s relative to ice. The separation between the two skaters after 5 seconds will be
30 m
32 m
40 m
28 m
The correct Answer is:A
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the Situation
We have two skaters, A and B, with masses M and 2M respectively, standing together on a frictionless ice surface. They push each other apart.
Step 2: Identify the Given Information
- Mass of skater A = M
- Mass of skater B = 2M
- Speed of skater B (relative to ice) = 2 m/s
- Time after which we need to find the separation = 5 seconds
Step 3: Apply Conservation of Momentum
Since there are no external forces acting on the system, the total momentum before and after the skaters push off each other must be conserved.
- Initial momentum (before they push off) = 0 (both are at rest)
- Final momentum = momentum of A + momentum of B
Let the velocity of skater A after they push off be VA and the velocity of skater B be VB=2m/s.
Using conservation of momentum:
0=M⋅VA+2M⋅VB
Step 4: Substitute Known Values
Substituting VB=2m/s:
0=M⋅VA+2M⋅2
0=M⋅VA+4M
Step 5: Solve for VA
Rearranging the equation:
M⋅VA=−4M
Dividing both sides by M (assuming M ≠ 0):
VA=−4m/s
Step 6: Determine the Relative Velocity
The relative velocity between skater A and skater B is:
Vrelative=VA−VB=−4−2=−6m/s
The negative sign indicates that they are moving apart.
Step 7: Calculate the Separation After 5 Seconds
The distance (separation) between the two skaters after 5 seconds can be calculated using:
Distance=Relative Velocity×Time
Distance=6m/s×5s=30m
Final Answer
The separation between the two skaters after 5 seconds will be 30 meters.
---
We have two skaters, A and B, with masses M and 2M respectively, standing together on a frictionless ice surface. They push each other apart.
- Mass of skater A = M
- Mass of skater B = 2M
- Speed of skater B (relative to ice) = 2 m/s
- Time after which we need to find the separation = 5 seconds
Since there are no external forces acting on the system, the total momentum before and after the skaters push off each other must be conserved.
- Final momentum = momentum of A + momentum of B
0=M⋅VA+2M⋅VB
Substituting VB=2m/s:
0=M⋅VA+2M⋅2
0=M⋅VA+4M
Rearranging the equation:
M⋅VA=−4M
Dividing both sides by M (assuming M ≠ 0):
VA=−4m/s
The relative velocity between skater A and skater B is:
Vrelative=VA−VB=−4−2=−6m/s
The negative sign indicates that they are moving apart.
The distance (separation) between the two skaters after 5 seconds can be calculated using:
Distance=Relative Velocity×Time
Distance=6m/s×5s=30m
The separation between the two skaters after 5 seconds will be 30 meters.
Similar Questions
Two blocks of masses M1andM2 are placed in contact with each other on a frictionless horizontal surface. If a force F is applied on the block of mass M1, what is the contact force between the two blocks?
View SolutionTwo particles of masses m and M are initially at rest at an infinite distance apart. They move towards each other and gain speeds due to gravitational attraction. Find their speeds when the separation between the masses becomes equal to d.
View SolutionTwo men A and B of masses 50kg and 20g respectively are at rest on a frictionless surface as shown in figure. If A pushes B with relative velocity 0.7m/s then find velocity of A just after the push.
_2019_CBT7_E01_018_Q01.png)
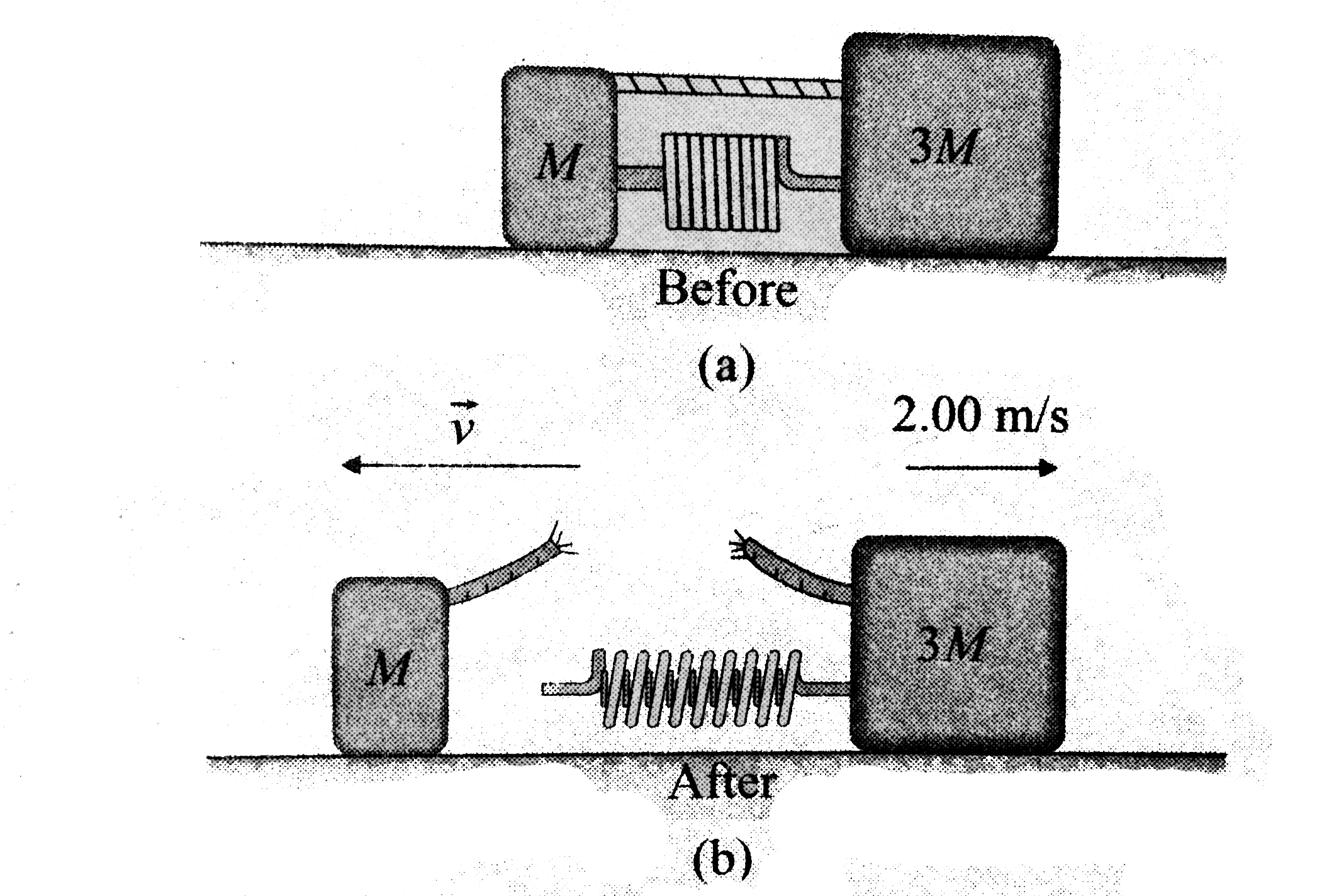
View SolutionTwo blocks of masses M and 3M are placed on a horizontal, frictionless surface. A light spring is attached to one of them and the blocks are pushed together with the spring between them. A cord initially holding the blocks together is burned, after that, the block of mass 3M moves to the right with a speed of 2.00m/s. (a) What is the velocity of the block of mass M. (b) Find the system's original elastic potential energy, taking M=0.350kg. (c) Is the original energy in the spring or in the cord? Explain your answer. (d) Is momentum of the system conserved in the bursting apart process? How can it be with large forces acting? How can it be with no motion beforehand and plenty of motion afterward?
View SolutionTwo particles of masses 2m and 3m are placed at separation d on a smooth surface. They move towards each other due to mutual attractive force. Find (a) acceleration of c.m. (b) Velocity of c.m. when separation between particles becomes d/3. ( c) At what distance from the initial position of mass 2m, the particles collide.
View SolutionA skater of mass m standing on ice throws a stone of mass M with a velocity of v in a horizontal direction. The distance over which the skater will move back (the coefficient of friction between the skater and the ice is μ)
View SolutionTwo skaters have weight in the ratio 4:5 and are 9m apart, on a smooth frictionless surface. They pull on a rope stretched between them. The ratio of the distance covered by them when they meet each other will be
View SolutionA man of mass m is standing on a platform of mass M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform with what velocity relative to the ice does the platform recoil?
View SolutionTwo particles of mass M and 2M are at a distance D apart. Under their mutual force of attraction they start moving towards each other. The acceleration of their centre of mass when they are D/2 apart is :
View SolutionA man of mass M stands at one end of a plank of length L Which lies at rest on a frictionless surface . The man walks to the other end of the plank. If the mass of the plank is 3M, the distance that the man moves relative to the ground is
View Solution
