Consider a situation where a cart carrying five boys is moving without friction due to inertia along a straight horizontal road, with a speed of 10 m/s. After travelling certain distance a boy jumps from the cart with a speed of 2 m/s with respect to cart in opposite direction to it. Then, second boy jumps with the same speed w.r.t. the cart, but in a perpendicular direction to the cart. The mass of the cart is 100 kg and mass of each boy is 20 kg.
Answer the following questions.
The speed of the cart after first boy has jumped out is
10 m/s
10.02 m/s
10.01 m/s
10.5 m/s
The correct Answer is:B
To solve the problem, we will use the principle of conservation of momentum. Let's break it down step by step.
1. Identify the Initial Conditions:
- The cart has a mass of mc=100kg.
- Each boy has a mass of mb=20kg.
- There are 5 boys, so the total mass of the boys is 5×20=100kg.
- The total mass of the system (cart + boys) is mtotal=mc+100kg=200kg.
- The initial speed of the cart is v0=10m/s.
2. Calculate the Initial Momentum:
- The initial momentum pinitial of the system is given by:
pinitial=mtotal×v0=200kg×10m/s=2000kg m/s
3. Consider the First Boy Jumping Off:
- When the first boy jumps off with a speed of 2m/s in the opposite direction to the cart's motion, his velocity with respect to the ground becomes:
vboy=v0−2=10m/s−2m/s=8m/s(in the negative direction)
4. Calculate the Final Momentum After the Boy Jumps:
- After the boy jumps, the mass of the cart becomes 100kg+80kg=180kg (since there are now 4 boys left).
- Let vf be the final speed of the cart after the boy jumps off. The final momentum pfinal is given by:
pfinal=(mc+80)vf+mbvboy=180vf+20(−8)
- This simplifies to:
pfinal=180vf−160
5. Set Initial Momentum Equal to Final Momentum:
- By the conservation of momentum:
pinitial=pfinal
2000=180vf−160
6. Solve for vf:
- Rearranging the equation gives:
180vf=2000+160
180vf=2160
vf=2160180=12m/s
Final Answer:
The speed of the cart after the first boy has jumped out is 12m/s.
- The cart has a mass of mc=100kg.
- Each boy has a mass of mb=20kg.
- There are 5 boys, so the total mass of the boys is 5×20=100kg.
- The total mass of the system (cart + boys) is mtotal=mc+100kg=200kg.
- The initial speed of the cart is v0=10m/s.
- The initial momentum pinitial of the system is given by:
pinitial=mtotal×v0=200kg×10m/s=2000kg m/s
- When the first boy jumps off with a speed of 2m/s in the opposite direction to the cart's motion, his velocity with respect to the ground becomes:
vboy=v0−2=10m/s−2m/s=8m/s(in the negative direction)
- After the boy jumps, the mass of the cart becomes 100kg+80kg=180kg (since there are now 4 boys left).
- Let vf be the final speed of the cart after the boy jumps off. The final momentum pfinal is given by:
pfinal=(mc+80)vf+mbvboy=180vf+20(−8)
- This simplifies to:
pfinal=180vf−160
- By the conservation of momentum:
pinitial=pfinal
2000=180vf−160
- Rearranging the equation gives:
180vf=2000+160
180vf=2160
vf=2160180=12m/s
The speed of the cart after the first boy has jumped out is 12m/s.
Similar Questions
Momentum is the ability of imparting or tending to import motion to other bodies. The total momentum of a system remains conserved if no external force is acting it. This is calculated by the formula →p=m→v.
Consider a situation where a cart carrying five boys is moving without friction due to inertia along a straight horizontal road, with a speed of 10 m/s. After travelling certain dfistance a boy jumps from the cart with a speed of 2 m/s with respect to cart in opposite direction to it. Then, second boy jumps with the same speed w.r.t. the cart, but in a perpendicular direction to the cart. The mass of the cart is 100 kg and mass of each boy is 20 kg.
Answer the following questions.
The speed of the cart after second boy jumps will
View SolutionTwo boys cycling on the road with the same speed are ......... relative to each other.
View SolutionA cart is moving horizontally along a straight line with constant speed 30ms−1. A particle is to be fired vertically upwards from the moving cart in such a way that it returns to the cart at the same point from where it was projected after the cart has moved 80m. At what speed (relative to the cart) must the projectile be fired? (Take g=10ms−2)
View SolutionA cart is moving horizontally along a straight line with constant speed 30ms−1. A particle is to be fired vertically upwards from the moving cart in such a way that it returns to the cart at the same point from where it was projected after the cart has moved 80m. At what speed (relative to the cart) must the projectile be fired? (Take g=10ms−2)
View SolutionA cart is moving horizontally along a straight line with constant speed 30 m/s. A projectile is to be fired from the moving cart in such a way that it will return to the cart after the cart has moved 120m. At what speed (relative to the cart, in m/s) must the projectile be fired ? (Take g=10m/s2)
View SolutionA cart moves with a constant speed along a horizontal circular path. From the cart, a particle is thrown up vertically with respect to the cart.
View SolutionA cart A of mass 50 kg moving at a speed of 20 km/h hits a lighter cart B of mass 20 kg moving towards it at a speed of 10 km/h. The two carts cling to each other. Find the speed of the combined mass after the collision.
View SolutionA bob of mass m is hanging from a cart of mass M. System is relased from rest from the position shown. Find the maximum speed of the cart with respect to ground.
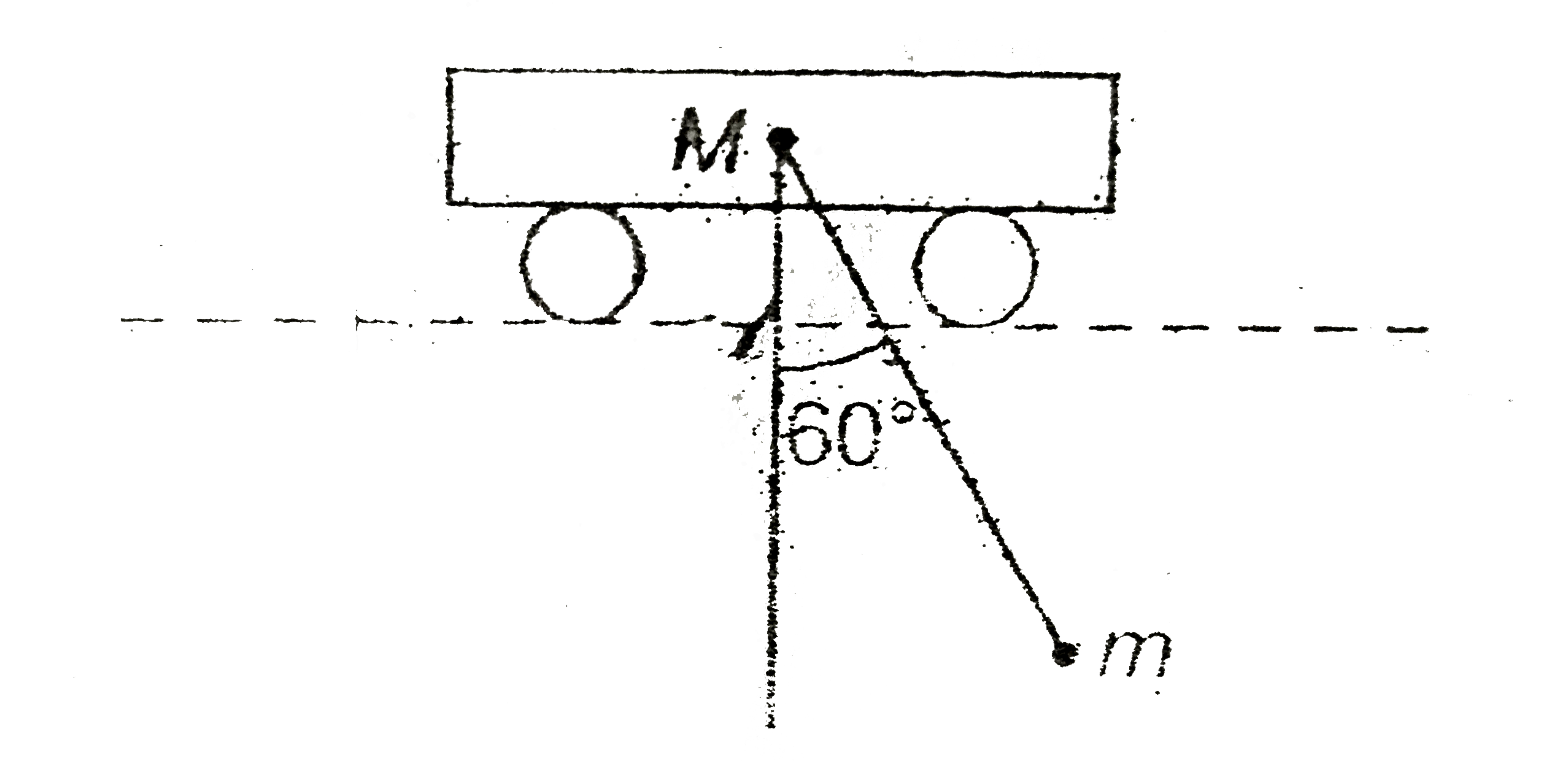
View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
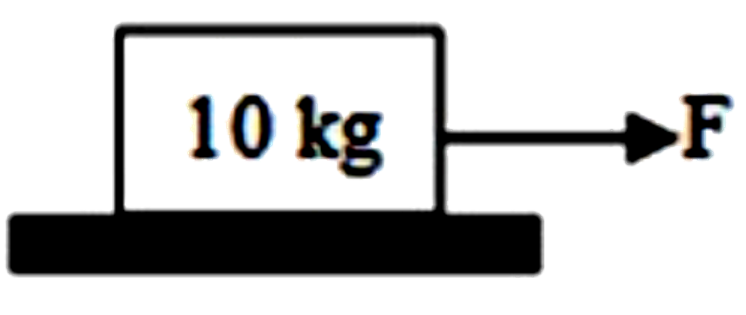
View SolutionA force F=2t2 is applied to the cart of mass 10 Kg, initially at rest. The speed of the cart at t = 5 s is -
View Solution