A ring of mass m and radius a is connected to an inextensible string which passes over a frictionless pulley. The other end of string is connected to upper end of a massless spring of spring constant k. The lower end of the spring is fixed. The ring can rotate in the vertical plane about hinge without any friction. If horizontal position of ring is equilibrium position then find time period of small in oscillations of the ring.
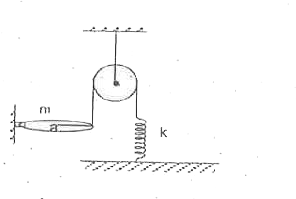
When displacement of the ring is θ, then extension in spring =(2aθ+x0)
Energy of system
E=12k(2aθ+x0)2−mgaθ+12l(dθdt)2
E=12k(2aθ+x0)2−mgaθ+12(12ma2+ma2)(dθdt)2
⇒dEdt=k(2aθ+x0)2adθdt−mgadθdt+32ma2(dθdt)d2θdt2
As dEdt=0,k(2aθ+x0)2a−mga=−32ma2d2θdt2
4akθ+2akx0−mga=−32ma2d2θdt2
∴83kmθ=−d2θdt2
∴ω=√8k3m
∴T=2π√3m8k
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View Solution
Knowledge Check
A 10 kg mass is connected at one end of a massless spring with force constant k = 1000 N/m, keeping other end fixed in a horizontal plane as shown in the fig. 15.6
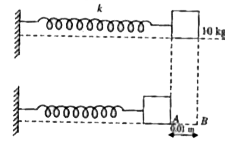 If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2
If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2
A uniform semicircular ring of mass m and radius r is hinged at end A so that it can rotate freely about end A in the vertical plane as shown in the figure. Calculate angle made by line AB with vertical in equilibrium position and time period of small oscillation of ring.

View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionA mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200Nm the other end of which is fixed to a rigid support. Study the following statements.
View SolutionA light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View SolutionTwo masses of 3 kg and 4 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.
View Solution
