A particle of mass 4g performs S.H.M. between x=−10cmandx=+10 cm along x-axis with frequency 60Hz, initially the particle is at x = +5 cm. Find
velocity-displacement and acceleration displacement curve of this motion.
To solve the problem, we will derive the velocity-displacement and acceleration-displacement curves for a particle performing Simple Harmonic Motion (SHM) with the given parameters.
1. Identify the Parameters:
- Mass of the particle, m=4g=0.004kg (not needed for the curves).
- Amplitude, A=10cm=0.1m.
- Frequency, f=60Hz.
2. Calculate Angular Frequency:
ω=2πf=2π×60=120πrad/s
3. Velocity-Displacement Relationship:
The velocity v in SHM is given by the formula:
v=ω√A2−x2
Substituting the values:
v=120π√(0.1)2−x2=120π√0.01−x2
4. Acceleration-Displacement Relationship:
The acceleration a in SHM is given by the formula:
a=−ω2x
Substituting the value of ω:
a=−(120π)2x=−14400π2x
5. Sketching the Curves:
- Velocity-Displacement Curve: The velocity will be maximum at the amplitude (±0.1 m) and zero at the extreme points (±0.1 m). The curve will be a semi-ellipse shape, starting from the maximum velocity at the amplitude and decreasing to zero at the extremes.
- Acceleration-Displacement Curve: The acceleration will be linear with respect to displacement, starting from zero at the equilibrium position (x = 0) and reaching maximum negative values at the extremes (±0.1 m). The slope of this line is given by −14400π2.
Final Formulas:
- Velocity-Displacement:
v=120π√0.01−x2
- Acceleration-Displacement:
a=−14400π2x
- Mass of the particle, m=4g=0.004kg (not needed for the curves).
- Amplitude, A=10cm=0.1m.
- Frequency, f=60Hz.
ω=2πf=2π×60=120πrad/s
The velocity v in SHM is given by the formula:
v=ω√A2−x2
Substituting the values:
v=120π√(0.1)2−x2=120π√0.01−x2
The acceleration a in SHM is given by the formula:
a=−ω2x
Substituting the value of ω:
a=−(120π)2x=−14400π2x
- Velocity-Displacement Curve: The velocity will be maximum at the amplitude (±0.1 m) and zero at the extreme points (±0.1 m). The curve will be a semi-ellipse shape, starting from the maximum velocity at the amplitude and decreasing to zero at the extremes.
- Acceleration-Displacement Curve: The acceleration will be linear with respect to displacement, starting from zero at the equilibrium position (x = 0) and reaching maximum negative values at the extremes (±0.1 m). The slope of this line is given by −14400π2.
- Velocity-Displacement:
v=120π√0.01−x2
- Acceleration-Displacement:
a=−14400π2x
Similar Questions
A particle executes SHM with an amplitude 8cm and a frequency 4Hz initially, in the positive direction , determine its displacement equation and the maximum velocity and acceleration.
View SolutionThe equation of S.H.M. of a particle is a+4π2x=0, where a is instantaneous linear acceleration at displacement x. Then the frequency of motion is
View SolutionThe displacement of a particle along the x-axis is given by x=3+8t+7t2. Obtain its velocity and acceleration at t=2s.
View SolutionA particle executes SHM with an amplitude of 10cm and frequency 2Hz, at t=0, the particle is at point where potential energy and kinetic energy are same. Find the equation of displacement of particle.
View SolutionThe velocity of any particle is related with its displacement As, x=√v+1, Calculate acceleration at x=5m.
View SolutionA particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.
View SolutionThe force of a particle of mass 1 kg is depends on displacement as F = —4x then the frequency of S.H.M. is
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
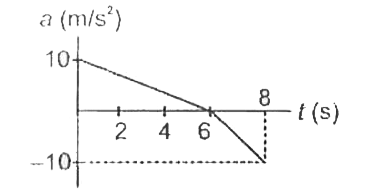
View SolutionA particle executes shm with an amplitude of 10 cm and a period of 5 s. Find the velocity and acceleration of the particle of a distance 5 cm from the equilibrium position.
View SolutionA body of mass 8 kg performs S.H.M. of amplitude 60 cm. The restoring force is 120 N, when the displacement is 60 cm. The time period is
View Solution