The velocity of any particle is related with its displacement As, x=√v+1, Calculate acceleration at x=5m.
√6 unit
24 unit
240 unit
25 unit
The correct Answer is:A
To solve the problem, we need to find the acceleration of a particle given the relationship between its displacement x and its velocity v as x=√v+1. We will calculate the acceleration at x=5m.
1. Start with the given equation:
x=√v+1
2. Square both sides to eliminate the square root:
x2=v+1
3. Rearrange the equation to express v in terms of x:
v=x2−1
4. Now, we need to find the acceleration a. Recall that acceleration can be expressed as:
a=vdvdx
where dvdx is the derivative of velocity with respect to displacement.
5. Differentiate v with respect to x:
dvdx=ddx(x2−1)=2x
6. Substitute v and dvdx into the acceleration formula:
a=(x2−1)(2x)
7. Now, we need to find the acceleration at x=5m:
a=(52−1)(2⋅5)
=(25−1)(10)
=24⋅10
=240units
Final Answer:
The acceleration at x=5m is 240units.
---
x=√v+1
x2=v+1
v=x2−1
a=vdvdx
where dvdx is the derivative of velocity with respect to displacement.
dvdx=ddx(x2−1)=2x
a=(x2−1)(2x)
a=(52−1)(2⋅5)
=(25−1)(10)
=24⋅10
=240units
The acceleration at x=5m is 240units.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - EFFICIENT
50 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- MOCK TEST 9BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - PHYSICS (SECTION 2)
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
Similar Questions
The velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.
View SolutionVelocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
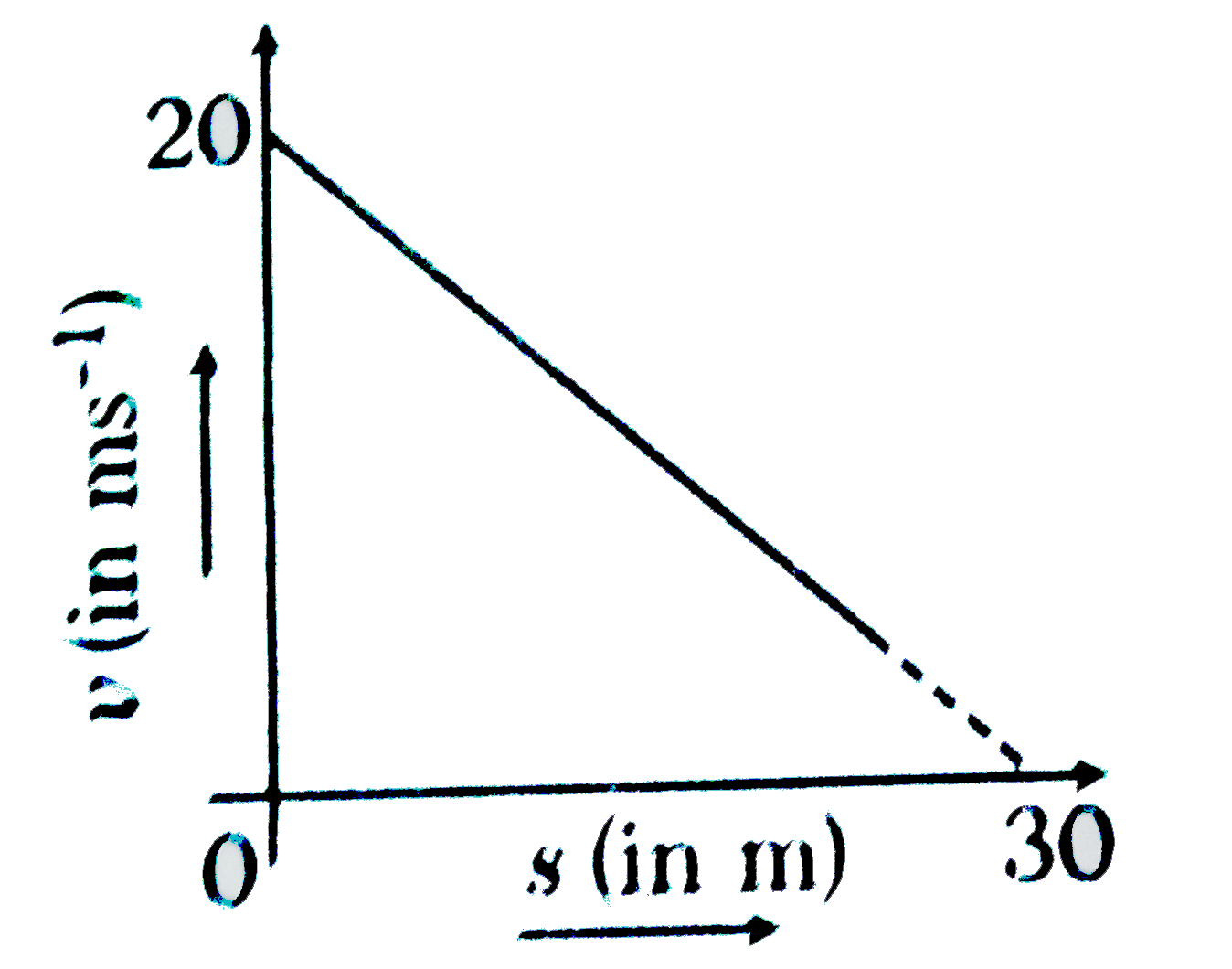
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
View SolutionThe intial velocity of a particle moving along x axis is u (at t = 0 and x = 0) and its acceleration a is given by a = kx. Which of the following equation is correct between its velocity (v) and position (x)?
View SolutionThe displacement 'x' and time of travel 't' for a particle moving an a straight line are related as t=√(x+1)(x−1). Its acceleration at a time t is
View SolutionFor motion of an object along the x-axis the velocity v dipends on the displacement x an v=3x2, then what is the acceleration at x=2m.
View SolutionThe position of a particle at any point instant is x . Find the velocity and acceleration at any instant .
View SolutionThe displacement x of a particle at the instant when its velocity v is given by v=√3x+16. Find its acceleration and initial velocity
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View Solution
