Draw the graph between displacement and
kinetic energy for a particle executing SHM.
To draw the graph between displacement and kinetic energy for a particle executing simple harmonic motion (SHM), we can follow these steps:
Step 1: Understand the Kinetic Energy Formula
The kinetic energy (KE) of a particle in SHM is given by the formula:
KE=12mω2(a2−x2)
where:
- m is the mass of the particle,
- ω is the angular frequency,
- a is the amplitude of the motion,
- x is the displacement from the mean position.
Step 2: Analyze the Relationship
From the formula, we can see that kinetic energy depends on the displacement x. Specifically, as x increases, KE decreases because of the term −x2. The maximum kinetic energy occurs when x=0 (the mean position).
Step 3: Determine Maximum Kinetic Energy
At x=0:
KEmax=12mω2a2
This is the maximum kinetic energy, which occurs when the particle is at the mean position.
Step 4: Identify the Shape of the Graph
Since the kinetic energy decreases as x increases from 0 to a (the amplitude), the graph of kinetic energy versus displacement will be a downward-opening parabola. The graph will reach its maximum at x=0 and will approach zero as x approaches a.
Step 5: Draw the Graph
1. Draw a coordinate system with:
- The x-axis representing displacement x (ranging from −a to a).
- The y-axis representing kinetic energy KE (starting from 0 up to KEmax).
2. Mark the maximum kinetic energy at x=0.
3. Draw a downward-opening parabola starting from the maximum kinetic energy at x=0 and approaching zero as x approaches a and −a.
Step 6: Label the Graph
Label the axes and the maximum kinetic energy point clearly.
Final Graph Representation
The graph will look like a downward parabola, starting from the maximum kinetic energy at the center (displacement = 0) and decreasing to zero at the maximum displacement (both positive and negative).
---
The kinetic energy (KE) of a particle in SHM is given by the formula:
KE=12mω2(a2−x2)
where:
- m is the mass of the particle,
- ω is the angular frequency,
- a is the amplitude of the motion,
- x is the displacement from the mean position.
From the formula, we can see that kinetic energy depends on the displacement x. Specifically, as x increases, KE decreases because of the term −x2. The maximum kinetic energy occurs when x=0 (the mean position).
At x=0:
KEmax=12mω2a2
This is the maximum kinetic energy, which occurs when the particle is at the mean position.
Since the kinetic energy decreases as x increases from 0 to a (the amplitude), the graph of kinetic energy versus displacement will be a downward-opening parabola. The graph will reach its maximum at x=0 and will approach zero as x approaches a.
1. Draw a coordinate system with:
- The x-axis representing displacement x (ranging from −a to a).
- The y-axis representing kinetic energy KE (starting from 0 up to KEmax).
2. Mark the maximum kinetic energy at x=0.
3. Draw a downward-opening parabola starting from the maximum kinetic energy at x=0 and approaching zero as x approaches a and −a.
Label the axes and the maximum kinetic energy point clearly.
The graph will look like a downward parabola, starting from the maximum kinetic energy at the center (displacement = 0) and decreasing to zero at the maximum displacement (both positive and negative).
Similar Questions
Draw the graph between displacement and
potential energy for a particle executing SHM.
View SolutionDraw the graph between displacement and
total energy for a particle executing SHM.
View SolutionEnergy of particle executing SHM depends upon
View SolutionWrite the relation between acceleration, displacement and frequency of a particle executing SHM.
View SolutionDraw a graph between displacement from mean position and time for a body executing free vibration in a vacuum.
View SolutionDraw a graph between displacement and time for a body executing natural vibrations.
View SolutionDisplacement between maximum potential energy position and maximum kinetic energy position for a particle executing S.H.M is
View SolutionAssertion : The graph of potential energy and kinetic energy of a particle in SHM with respect to position is a parabola.
Reason : Potential energy and kinetic energy do not vary linearly with position.
View SolutionIf a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
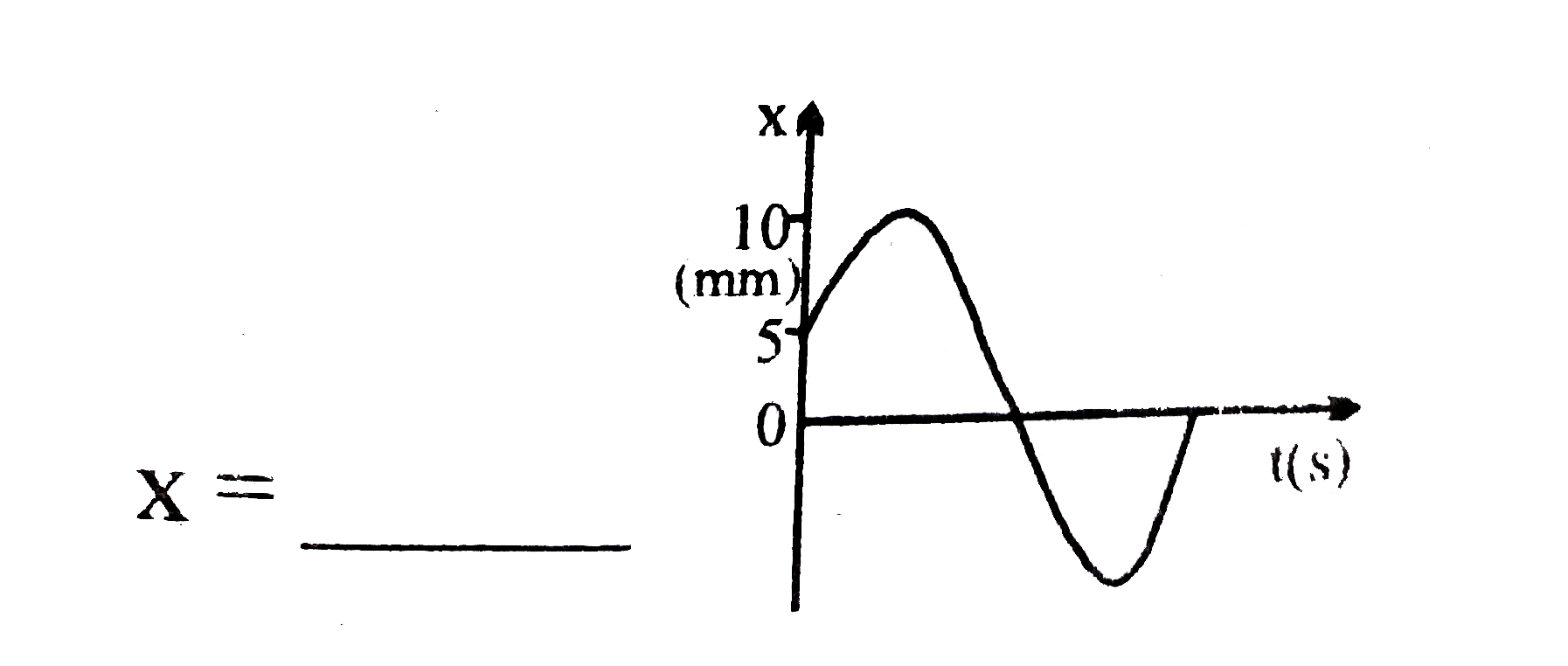
View Solution
