If a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
Straight line
Parabola
Ellipse
Hyperbola
The correct Answer is:3
To determine the nature of the graph plotted between velocity (v) and displacement (y) of a particle executing Simple Harmonic Motion (SHM) from the mean position, we can follow these steps:
1. Understand the relationship between velocity and displacement in SHM:
The velocity v of a particle in SHM can be expressed in terms of its displacement x from the mean position. The formula is:
v=ω√A2−x2
where ω is the angular frequency and A is the amplitude of the motion.
2. Square both sides of the equation:
To eliminate the square root, we square both sides:
v2=ω2(A2−x2)
3. Rearrange the equation:
Rearranging gives:
v2=ω2A2−ω2x2
This can be rewritten as:
v2+ω2x2=ω2A2
4. Identify the form of the equation:
The equation v2+ω2x2=ω2A2 resembles the standard form of an ellipse equation:
v2ω2A2+x2A2=1
This indicates that the relationship between v and x is elliptical.
5. Conclusion:
Therefore, when we plot the graph of velocity v against displacement x, the nature of the graph is an ellipse.
Final Answer:
The nature of the graph plotted between velocity (v) and displacement (y) of a particle executing SHM from the mean position is an ellipse.
---
The velocity v of a particle in SHM can be expressed in terms of its displacement x from the mean position. The formula is:
v=ω√A2−x2
where ω is the angular frequency and A is the amplitude of the motion.
To eliminate the square root, we square both sides:
v2=ω2(A2−x2)
Rearranging gives:
v2=ω2A2−ω2x2
This can be rewritten as:
v2+ω2x2=ω2A2
The equation v2+ω2x2=ω2A2 resembles the standard form of an ellipse equation:
v2ω2A2+x2A2=1
This indicates that the relationship between v and x is elliptical.
Therefore, when we plot the graph of velocity v against displacement x, the nature of the graph is an ellipse.
The nature of the graph plotted between velocity (v) and displacement (y) of a particle executing SHM from the mean position is an ellipse.
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION -D( Comprehension) )
3 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)
58 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
The shape of graph plotted between velocity and position of a particle executing simple harmonic motion is
View SolutionDraw the velocity-displacement graph of a body executing shm.
View SolutionWrite the relation between acceleration, displacement and frequency of a particle executing SHM.
View SolutionThe displacement of a particle executing SHM is given by
y=0.5 sin100t cm . The maximum speed of the particle is
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
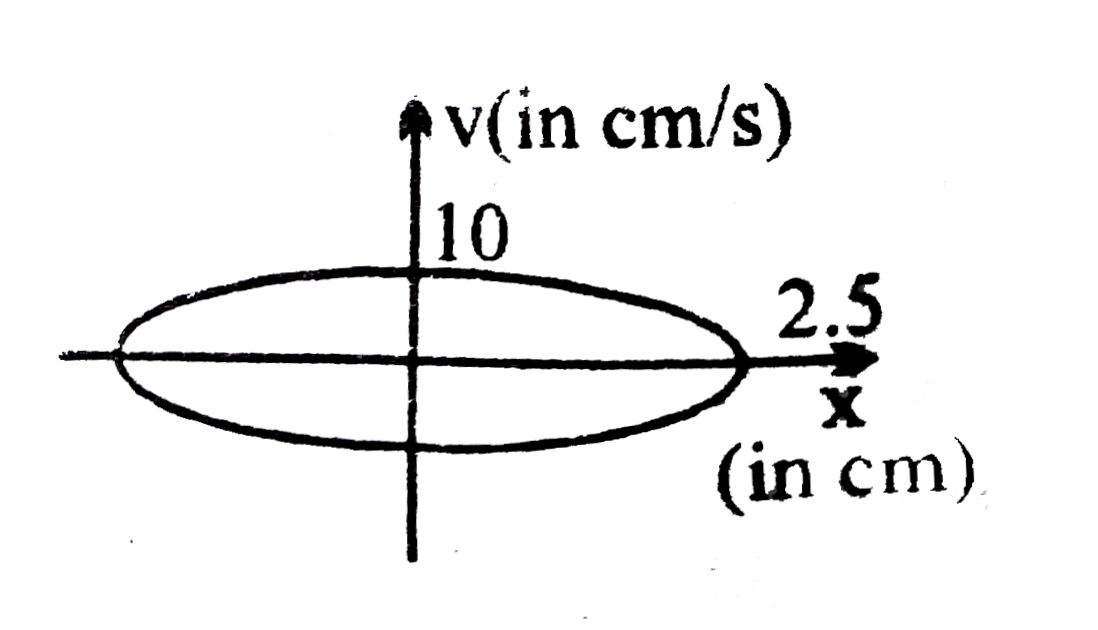
View SolutionDraw the graph between displacement and
kinetic energy for a particle executing SHM.
View SolutionDraw the graph between displacement and
potential energy for a particle executing SHM.
View SolutionThe displacement of a particle executing SHM is given by y=0.25 sin(200t) cm . The maximum speed of the particle is
View SolutionDraw the graph between displacement and
total energy for a particle executing SHM.
View SolutionThe graph shows the variation of displacement of a particle execting SHM with time . We infer from this graph that
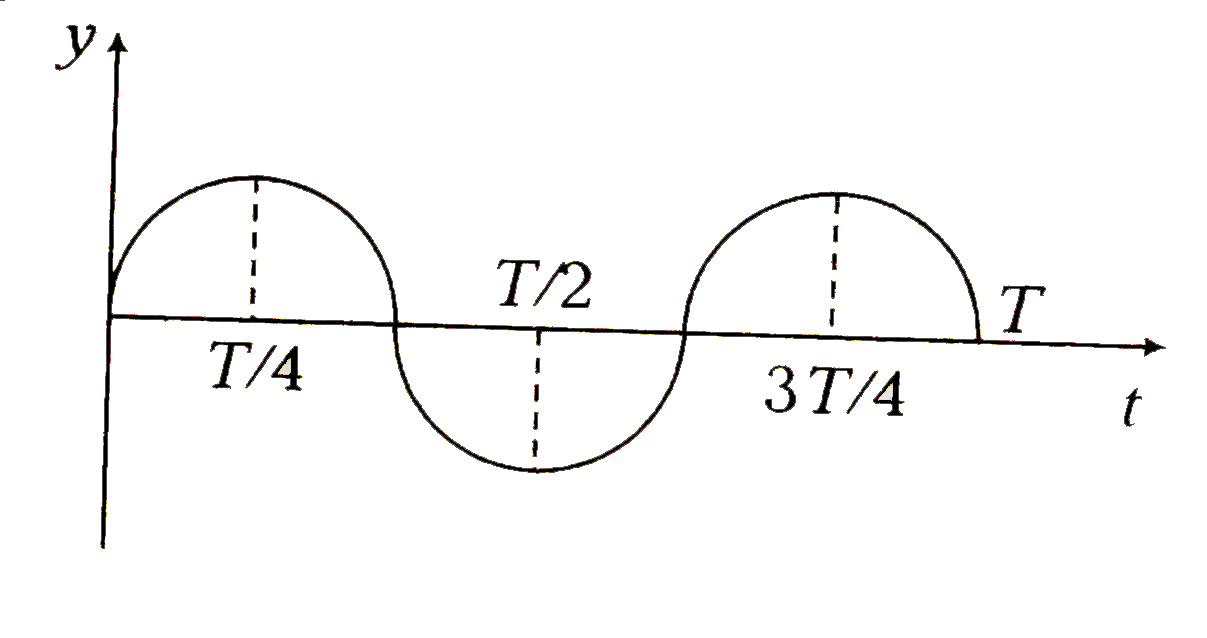
View Solution
