The slope of adiabatic curve is _________________than the slope of an isothermal curve.
The correct Answer is:Greater
To solve the question regarding the relationship between the slopes of adiabatic and isothermal curves, we can follow these steps:
1. Understand the Processes:
- The isothermal process occurs at a constant temperature, where the relationship between pressure (P) and volume (V) is given by the equation PV=C, where C is a constant.
- The adiabatic process occurs without heat exchange, and its relationship is described by the equation PVγ=K, where γ (gamma) is the heat capacity ratio (Cp/Cv) and K is a constant.
2. Derive the Slope for Isothermal Process:
- Starting with the isothermal equation PV=C, we can take the logarithm of both sides:
log(P)+log(V)=log(C)
- From this, we can differentiate to find the slope of the curve in a log-log plot:
d(log(P))d(log(V))=−1
- Therefore, the slope of the isothermal curve is -1.
3. Derive the Slope for Adiabatic Process:
- For the adiabatic process, we start with the equation PVγ=K. Taking the logarithm gives:
log(P)+γlog(V)=log(K)
- Differentiating this equation yields:
d(log(P))d(log(V))=−γ
- Thus, the slope of the adiabatic curve is -γ.
4. Compare the Slopes:
- Now we can compare the slopes derived from both processes:
- Slope of isothermal curve = -1
- Slope of adiabatic curve = -γ
- From this comparison, we can conclude that the slope of the adiabatic curve is steeper than that of the isothermal curve since γ (the heat capacity ratio) is greater than 1 for most gases.
5. Final Conclusion:
- Therefore, we can fill in the blank in the question: "The slope of the adiabatic curve is greater than the slope of an isothermal curve."
- The isothermal process occurs at a constant temperature, where the relationship between pressure (P) and volume (V) is given by the equation PV=C, where C is a constant.
- The adiabatic process occurs without heat exchange, and its relationship is described by the equation PVγ=K, where γ (gamma) is the heat capacity ratio (Cp/Cv) and K is a constant.
- Starting with the isothermal equation PV=C, we can take the logarithm of both sides:
log(P)+log(V)=log(C)
- From this, we can differentiate to find the slope of the curve in a log-log plot:
d(log(P))d(log(V))=−1
- Therefore, the slope of the isothermal curve is -1.
- For the adiabatic process, we start with the equation PVγ=K. Taking the logarithm gives:
log(P)+γlog(V)=log(K)
- Differentiating this equation yields:
d(log(P))d(log(V))=−γ
- Thus, the slope of the adiabatic curve is -γ.
- Now we can compare the slopes derived from both processes:
- Slope of isothermal curve = -1
- Slope of adiabatic curve = -γ
- From this comparison, we can conclude that the slope of the adiabatic curve is steeper than that of the isothermal curve since γ (the heat capacity ratio) is greater than 1 for most gases.
- Therefore, we can fill in the blank in the question: "The slope of the adiabatic curve is greater than the slope of an isothermal curve."
Similar Questions
Show that the slope of adiabatic curve at any point is Yama times the slope of an isothermal curve at the corresponding point.
View SolutionWhat is the slope for an isothermal process ?
View SolutionFor a p-V plot, the slope of an adiabatic curve = x × slope of isothermal at the same point. Here x is :
View SolutionShow that the adiabatic curve is steeper than the isothermal curve.
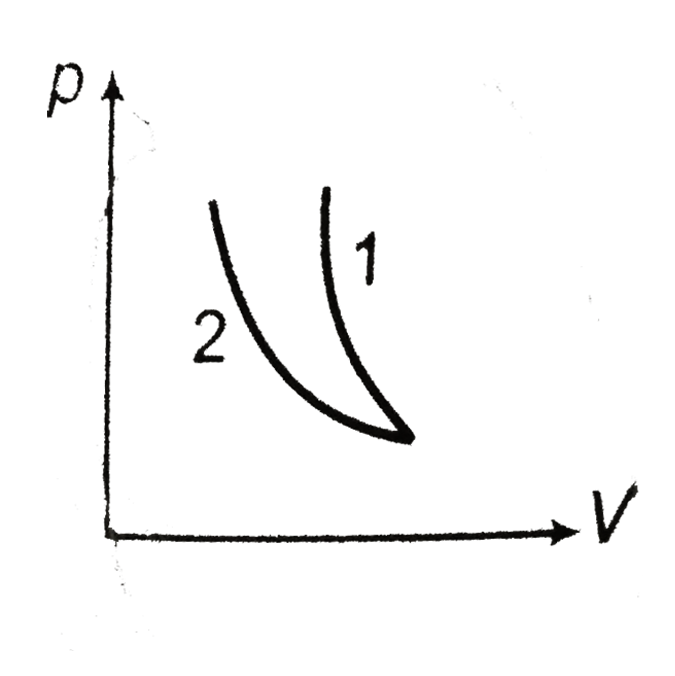
View SolutionAssertion: Isothermal and adiabatic, two processes are shown on p-V diagram. Process-1 is aidabatic and process-2 is isothermal.
Reason: At a given point, slope of adiabatic process =γ×slope of isothermal process.
View SolutionIf equation of the curve is y2=4x then find the slope of normal to the curve
View SolutionStatement-1: Temperature of a system can be increased without supplying heat.
Statement-2: If the initial volume of system is equal to final volume in a process then work done is necessarily zero.
Statement-3: If an adiabatic curve for a gas intersect with an isothermal curve for the same gas then at the point of intersection, the ratio of slope of the adiabatic and the isothermal curve is γ.
View SolutionThe activity of a certain radioactive sample is plotted against time in graph. If the initial slope of the curve is m, then find the slope of the curve at point P ?
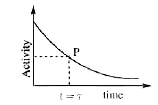
View SolutionShow that the slope of p−V diagram is greater for an adiabatic process as compared to an isothermal process.
View SolutionFind the equation of a curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.
View Solution
