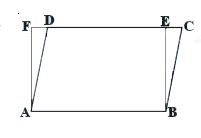
ABCD এবং ABEF দুটি সামান্তরিক। প্রমাণ করো, CDFE ও একটি সামান্তরিক।
Step by step video & image solution for ABCD এবং ABEF দুটি সামান্তরিক। প্রমাণ করো, CDFE ও একটি সামান্তরিক। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
ক্রয়মূল্য ও বিক্রয়মূল্যের অনুপাত 10:11 হলে, শতকরা লাভ -
03:23View Solutionಚಿತ್ರ ರಲ್ಲಿ ABCD, DCEF ಮತ್ತು ABEF ಗಳು ಸಮಾಂತರ ಚತುರ್ಭುಜಗಳು ಆದರೆ ವಿ (ADE) = ವಿ (BCF) ಎಂದು ಸಾಧಿಸಿ.
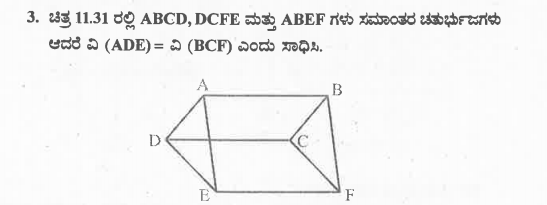 03:59View Solution
03:59View Solution2Ag(s)+Fe^(2+)(aq)rarr2Ag^+(aq)+Fe(s) বিক্রিয়াটি কী সম্ভব? ব্যাখ্যা করো। দেওয়া আছে, Fe^(2+)|Fe ও Ag^+|Ag তড়িদ্দ্বারের প্রমাণ বিজারণ বিভবের মান যথাক্রমে -0.44 ও +0.80V।
04:54View SolutionABCD is a parallelogram and ABEF is a rectangle Delta AFD ~= Delta BEC Show that.
06:27View SolutionABCD ఒక సమాంతర చతుర్భుజము ABEF ఒక దీర్ఘచతురస్రము DG, AB పైకి గీచిన లంబము అయిన (ABCD)వై||= (ABEF) వై|| అని చూపండి.
01:47View Solutionचित्र में ABCD और AFEB समान्तर चतुर्भुज हैं। सिद्ध कीजिए कि CDFE समान्तर चतुर्भुज हैं।
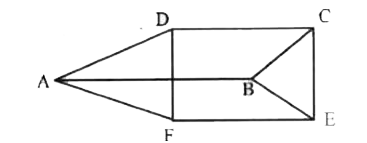 03:24View Solution
03:24View Solution[θ=srঅথবা কণ (বৃত্তীয় মানে )=(চাপ)/(ব্যাসার্ধ) ,সূত্র-সম্পর্কিত পেশ্নাবলি। ] দুটি বৃত্ত এমন যে, একটি অপরটি কেন্দ্রবিন্দুগামী। প্রথম বৃত্তের l দৈর্ঘ্যের চাপ তার কেন্দ্রে thetaএবংদ্বিতীয়বৃত্তেরmদৈর্ঘ্যেরচাপতারকেন্দ্রেphi সম্মুখ কোণ উৎপন্ন করে। প্রমাণ করাে যে, lphi=mtheta।
01:56View Solutionযদি |z1|=|z2|এবংarg z1 + arg z2 = 0হয়,তবেপ্রমাণকরোz1 = 1/(z2)।
03:06View Solutionযদি |z1|=|z2|এবংarg z1 ~ arg z2 = piহয়,তবেপ্রমাণকরোz1 + z2 = 0।
03:36View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
04:04View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG05:45View SolutionIn the adjacent figure ABCD is a parallelogram ABEF is a rectangle show that ΔAFD≅ΔBEC.
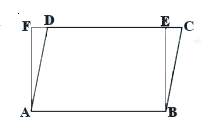 07:27View Solution
07:27View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG03:50View SolutionIn the adjacent figure ABCD is a parallelogram ABEF is a rectangle show that ΔAFD≅ΔBEC.
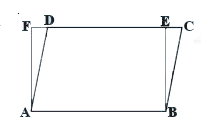 05:03View Solution
05:03View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG03:26View SolutionIn the adjacent figure ABCD is a parallelogram ABEF is a rectangle show that ΔAFD≅ΔBEC.
 04:39View Solution
04:39View Solution

