ABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG Solution in Bengali
Step by step video & image solution for ABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB. Prove that (i) ar (ABCD) = ar(ABEF) (ii) ar (ABCD) = AB xx DG by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
If 1cm represents 5m, what would be an area of 6 square cm. represent ?
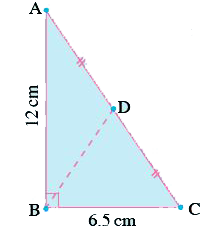
03:14View SolutionIn ΔABC,∠ABC=90∘,AD=DC,AB=12cmandBC=6.5 cm. Find the area of ΔADB .
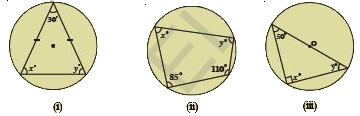
02:55View SolutionFind the values of x and y in the figures given below
01:34View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
03:43View Solutionआक्रति 9.13 में , ABCD एक समांतर चतुर्भुज है और EFCD एक आयत है ।
साथ ही , AL⊥DC है सिद्ध कीजिए कि
(i) ar(ABCD)=ar(EFCD)
(ii)(ABCD)=DC×AL
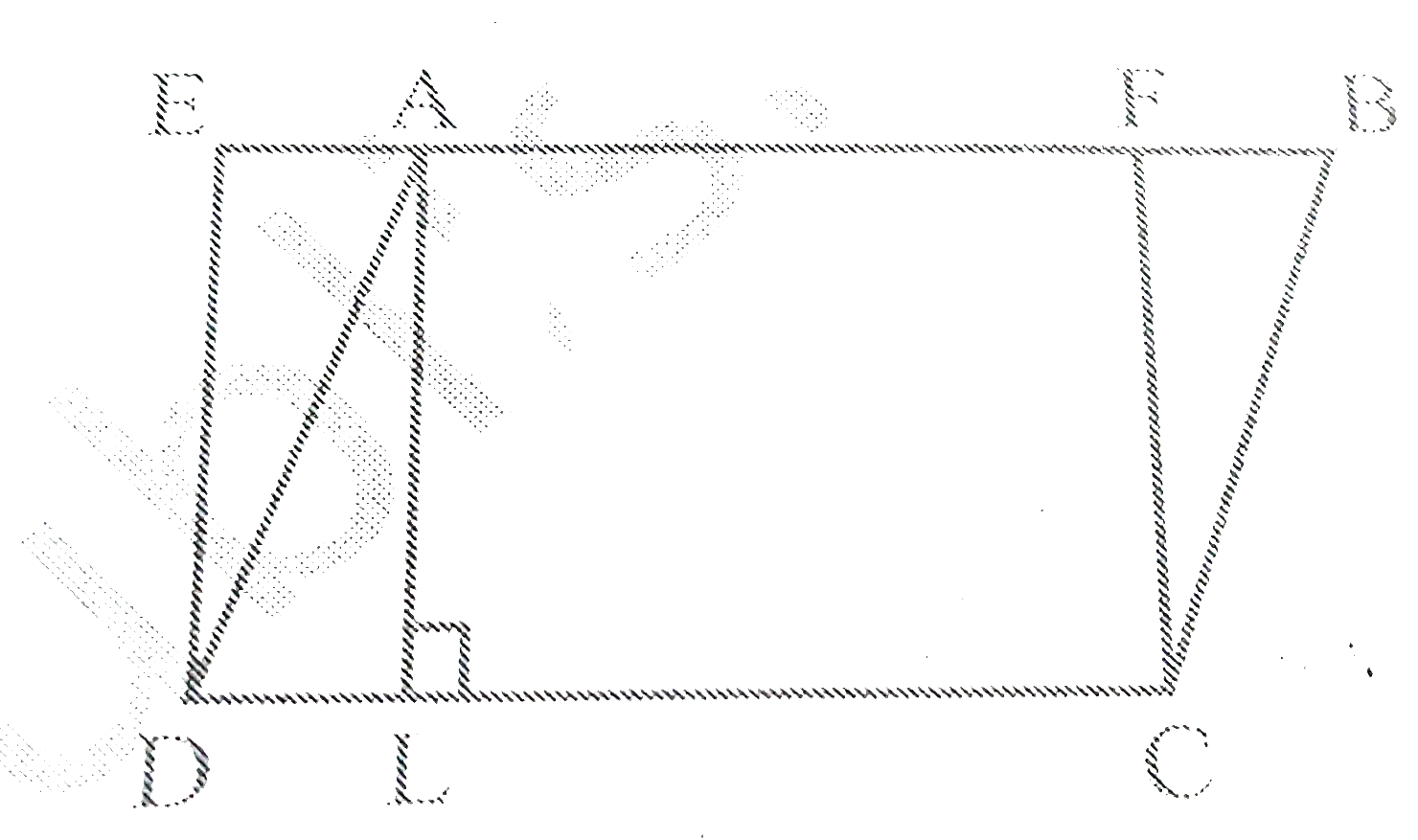
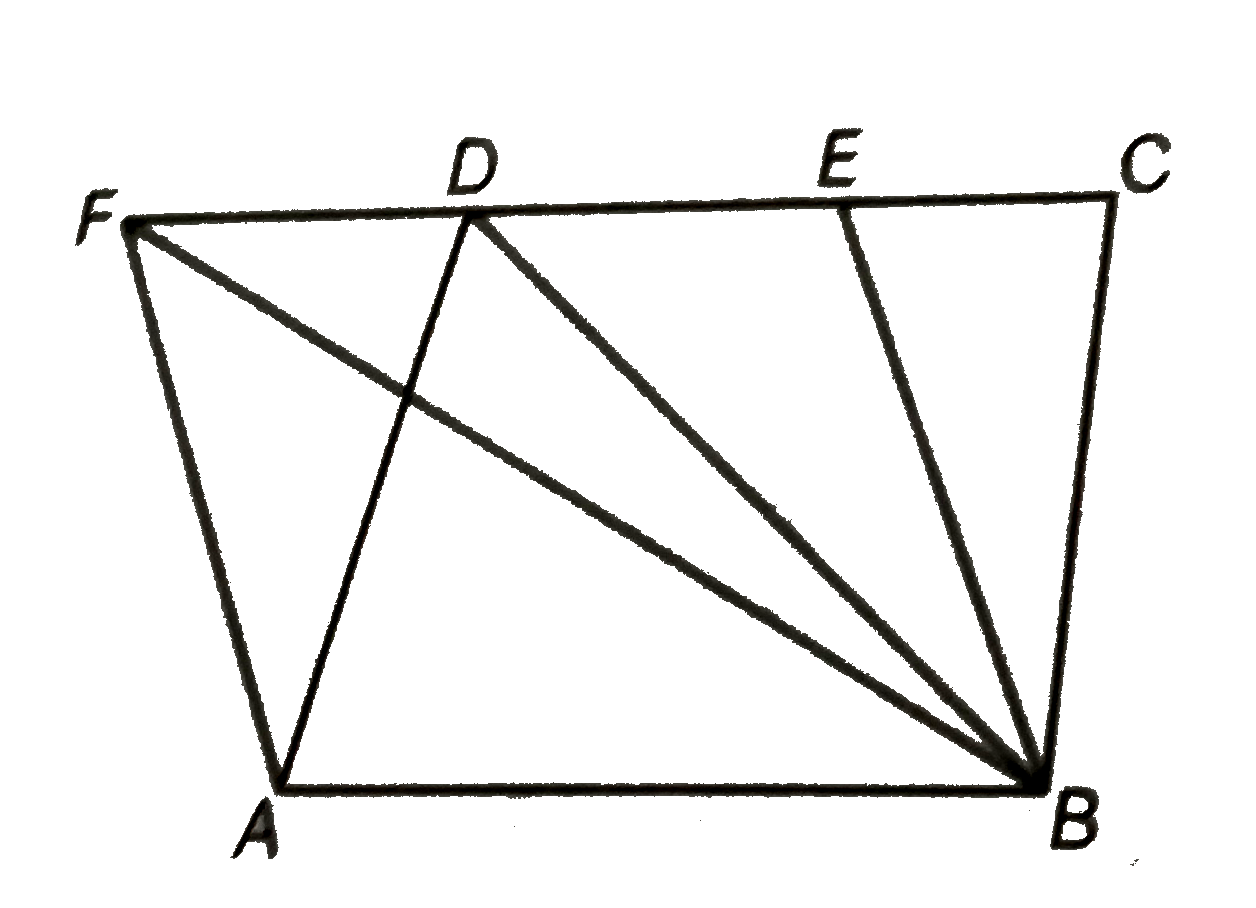
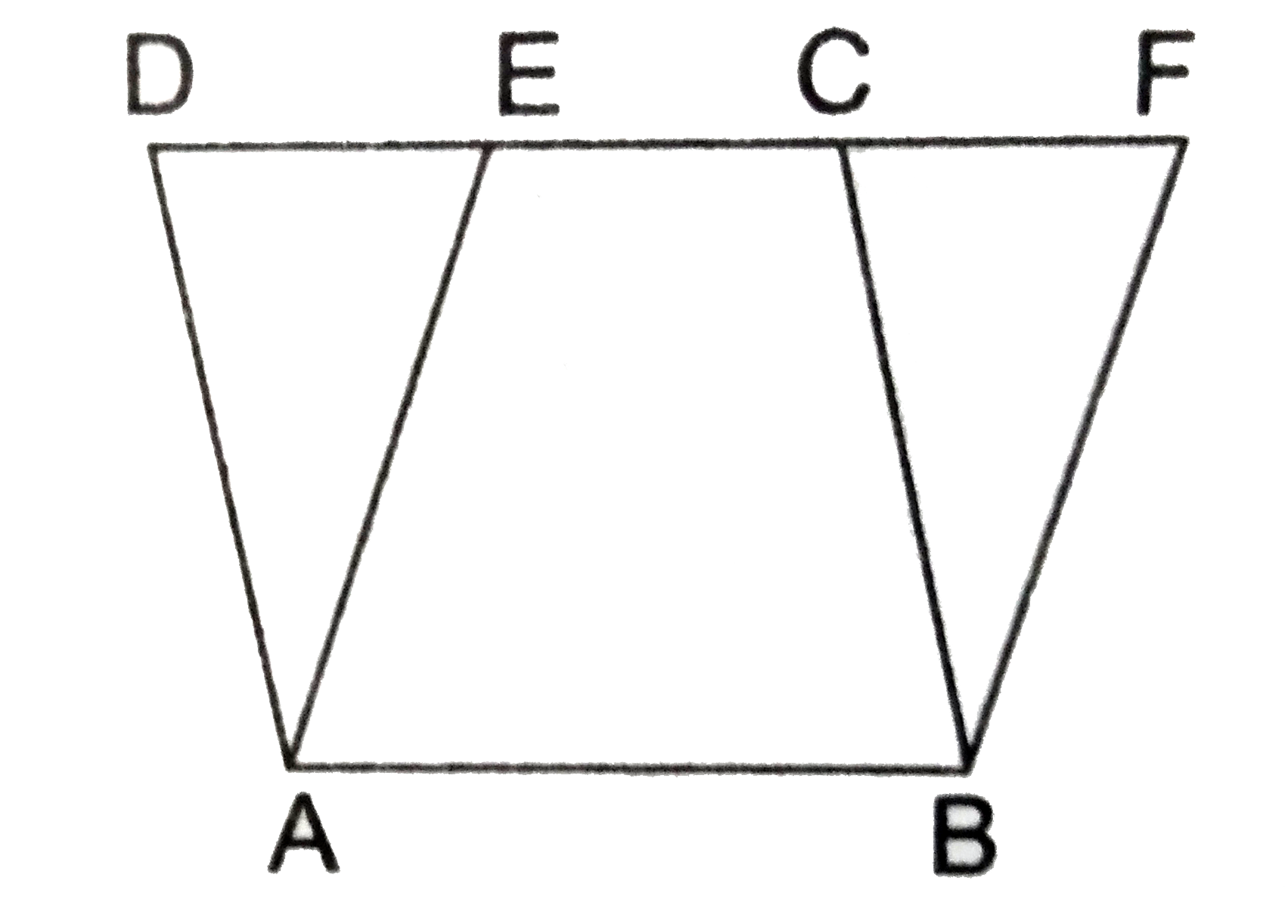
06:27View SolutionIn the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
07:16View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही AL⊥DC, तो सिद्ध कीजिए कि
(i)ar(ABCD)=ar(EFCD)
(ii)ar(ABCD)=DC×AL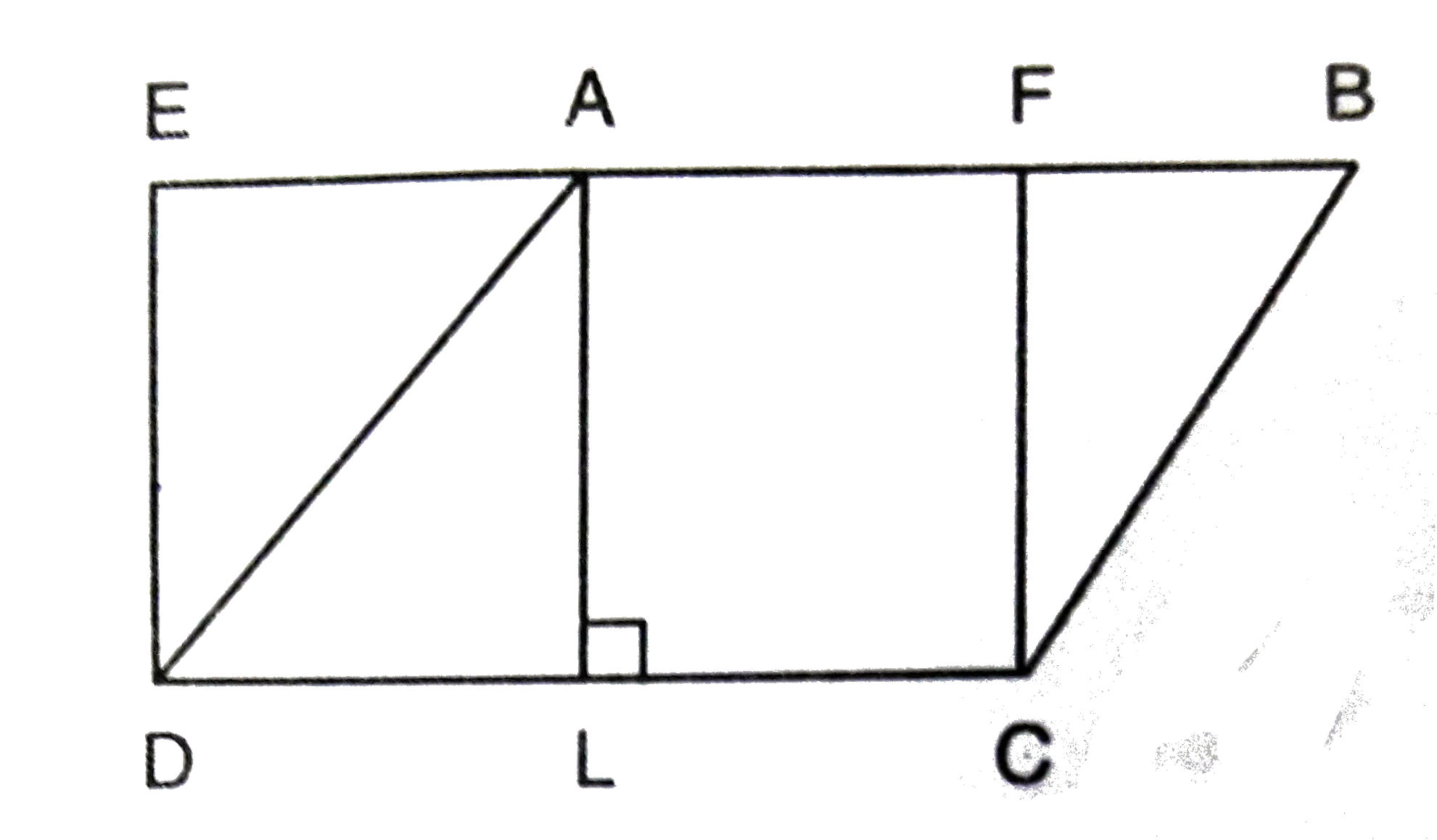
View SolutionABCD ఒక సమాంతర చతుర్భుజము ABEF ఒక దీర్ఘచతురస్రము DG, AB పైకి గీచిన లంబము అయిన (ABCD)వై||= (ABEF) వై|| అని చూపండి.
04:04View SolutionABCD ఒక సమాంతర చతుర్భుజము ABEF ఒక దీర్ఘచతురస్రము DG, AB పైకి గీచిన లంబము అయిన (ABCD)వై||=ABxDG వై|| అని చూపండి.
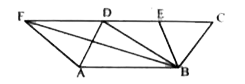
05:11View Solutionसमान्तर चतुर्भुज ABCD का क्षेत्रफल 90cm2 है। (आकृति देखिए) तो निम्नलिखित का क्षेत्रफल ज्ञात कीजिए।
(i)ar(ABEF) , (ii)ar(ABD) , (iii) ar(BEF)
09:39View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG04:15View SolutionTriangle ABC and parallelogram ABEF are on the same base, AB as in between the same parallels AB and EF. Prove that ar (ΔABC)=12 ar(|| gm ABEF)
05:03View SolutionTriangle ABC and parallelogram ABEF are on the same base, AB as in between the same parallels AB and EF. Prove that ar (ΔABC)=12 ar(|| gm ABEF)
05:22View SolutionTriangle ABC and parallelogram ABEF are on the same base, AB as in between the same parallels AB and EF. Prove that ar (ΔABC)=12 ar(|| gm ABEF)
04:39View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG06:41View Solution