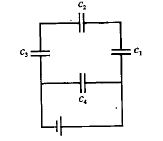
આકૃતિમાં C1=C2=C3=C4=10μF તથા બેટરીનો ટર્મિનલ વોલ્ટેજ 500 V છે.બેટરીના બે છેડાઓ વચ્ચે આવેલા નેટવર્કનું સમતુલ્ય કેપેસીટન્સ શોધો.

Step by step video & image solution for આકૃતિમાં C_1 = C_2 = C_3 = C_4 = 10 muF તથા બેટરીનો ટર્મિનલ વોલ્ટેજ 500 V છે.બેટરીના બે છેડાઓ વચ્ચે આવેલા નેટવર્કનું સમતુલ્ય કેપેસીટન્સ શોધો. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
કાર્બન (C ), સિલિકોન (Si) અને જમેનિયમ (Ge) ના સ્ફટિકમય બંધારણો સમાન છે, છતા શા માટે કાર્બન, અવાહક તરીકે અને સિલિકોન તથા જર્મેનિયમ આંતરિક અર્ધવાહકો તરીકે વર્તે છે ?
View SolutionFind the charges on the three capacitors connected to a bettery as shown in figure (31.E1). Take C1=2.0=2.0,μF,C2=4.0,μf,C3=6.0,μFandV=12vo<s.(31-E1). Take C1=2.0μF,C2=4.0μF,C2=6.0μFandV=12vo<s.

View SolutionFind the charges on the three capacitors connected to a bettery as shown in figure (31.E1). Take C1=2.0=2.0,μF,C2=4.0,μf,C3=6.0,μFandV=12vo<s.(31-E1). Take C1=2.0μF,C2=4.0μF,C2=6.0μFandV=12vo<s.

View SolutionC0C1+C1C2+C2C3+…+Cn−1Cn=
View SolutionIf C1,C2,C3,C4 are the coefficients of any consecutive terms in the expansion of (1+x)n , prove that :
C1C1+C2+C3C3+C4=2C2C2+C3
View SolutionEvaluate 10C1+10C2+10C3+………+10C10
View Solution(.21C1−.10C1)+(.21C2−.10C2)+(.21C3−.10C3)+(.21C4−.10C4) +….+ (.21C10−.10C10) का मान है
View SolutionProve that (C0+C1)(C1+C2)(C2+C3)(C3+C4)...........(Cn−1+Cn) = C0C1C2.....Cn−1(n+1)nn!
View SolutionFind the charges on the three capacitors connected to a bettery as shown in figure (31.E1). Take C1=2.0=2.0,μF,C2=4.0,μf,C3=6.0,μFandV=12vo<s.(31-E1). Take C1=2.0μF,C2=4.0μF,C2=6.0μFandV=12vo<s.

View SolutionA network of four capacitors of edacity equal to c1=c,c2=2c,c3=3c and c4=4c are connected to a battery as in figure. The ratio of the chaises on c2 and c4 is:
View Solutionउस अवकल समीकरण की कोटि, जिसका व्यापक हल t=(C1+C2)cos(x+C3)−C4ex+C5, है, जहाँ C1,C2,C3,C4,C5 स्वेच्छ अचर हैं, है
View SolutionThe order of the differental equation whose general solution is given by y=(C1+C2)cos(x+C3)−C4ex+C5, where C1,C2,C3,C4,C5 are arbitrary constant is
View Solution(C0+C1)(C1+C2)(C2+C3)(C3+C4)...........(Cn−1+Cn)=
C0C1C2.....Cn−1(n+1)nn!
View SolutionUsing binomial theorem (without using the formula for ^nCr ) , prove that nC4+mC2−mCn1C2=mC4−m+nCm1C3+m+nCm2C2−m+nCm3C1+m+nC4.
View SolutionEvaluate |^x C_1^x C_2^x C_3^y C_1^y C_2^y C_3^z C_1^z C_2^z C_3|
View Solution
