Match the moment of inertia of the rods with given mass and length in column A about the given axis 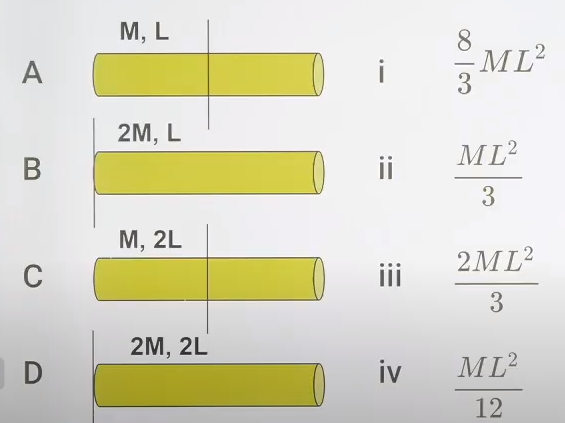
A(iv),B(iii),C(ii),D(i)
A(ii),B(iii),C(iv),D(i)
A(iii),B(ii),C(iv),D(i)
A(ii),B(iv),C(i),D(iii)
Step by step video & image solution for Match the moment of inertia of the rods with given mass and length in column A about the given axis by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
Knowledge Check
Match the following:
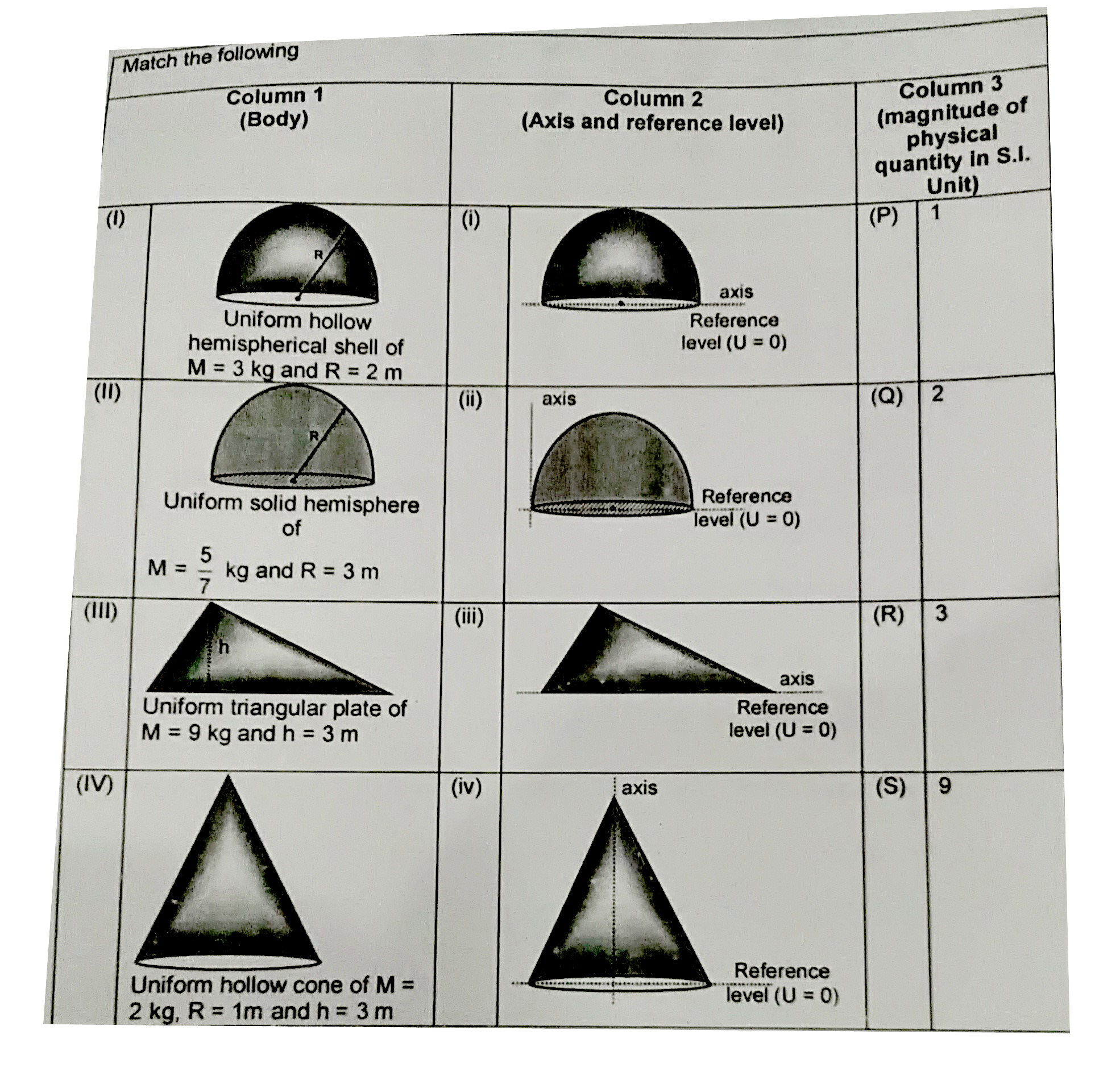
Moment of inertia of body (in kg−m2) (shown in column -1) about the axis (shown in column -2)A(I)(i)(S)B(II)(ii)(S)C(III)(iii)(Q)D(IV)(iv)(R)The moment of inertia of a system of four rods each of length l and mass m about the axis shown is
 A23ml2B2ml2C3 ml2D83ml2
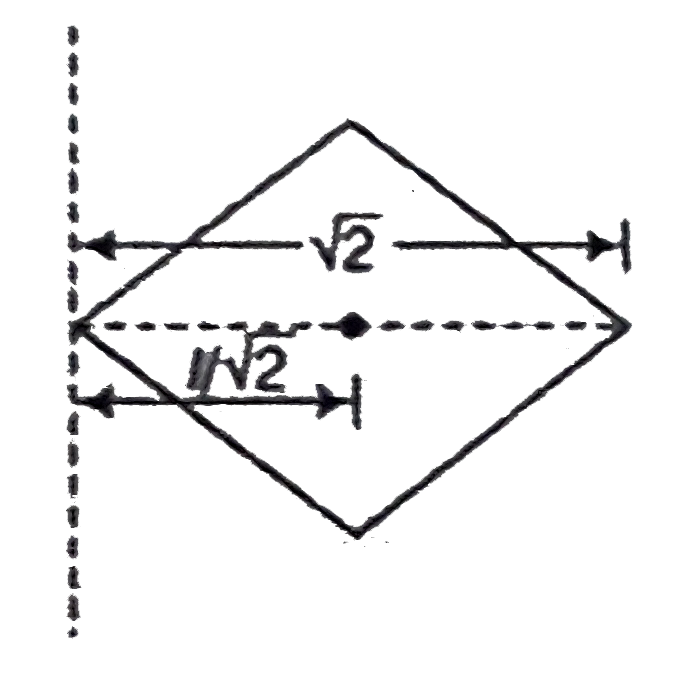
A23ml2B2ml2C3 ml2D83ml2The moment of inertia of a thin sheet of mass M of the given shape about the specified axis is
 A(3/2)MR2B(3/4)MR2CMR2(1+1/√2)DMR2/(2√2)
A(3/2)MR2B(3/4)MR2CMR2(1+1/√2)DMR2/(2√2)
Calculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View SolutionCalculate the moment of inertia of the given rod about an axis CD.
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.

View SolutionThe moment of inertia of thin rod of linear density λ and length l about an axis passing through one end and perpendicular to its length is
View Solution