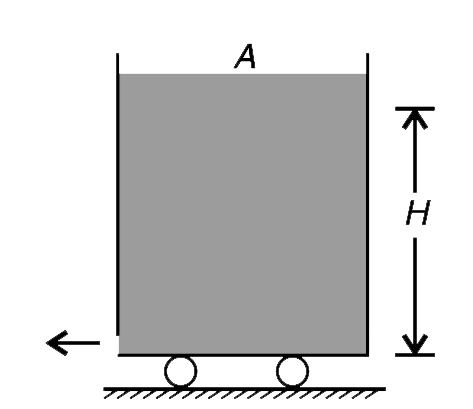
A cylindrical massless container of cross sectional area A have a fluid filled up to height h and have a small orifice of area a in wall near its bottom. Find minimum coefficient between container and ground so that container does not move

$\frac{2 a}{A}$

$\frac{a}{2 A}$

$\frac{A}{a}$

none

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem of finding the minimum coefficient of friction between the container and the ground so that the container does not move, we can follow these steps:
Step 1: Understand the System
We have a cylindrical massless container filled with a fluid up to a height $h$ . The container has a cross-sectional area $A$ and a small orifice with area $a$ at the bottom.
Step 2: Calculate the Weight of the Fluid
The weight of the fluid in the container can be calculated using the formula:
$Weight = mass \times g = ρ \cdot A \cdot h \cdot g$
where:
- $ρ$ is the density of the fluid,
- $A$ is the cross-sectional area of the container,
- $h$ is the height of the fluid,
- $g$ is the acceleration due to gravity.
Step 3: Determine the Velocity of Efflux
Using Torricelli's theorem, the velocity $v$ of the fluid exiting the orifice can be expressed as:
$v = \sqrt{2 g h}$
Step 4: Calculate the Force Due to Efflux
The force exerted by the fluid exiting through the orifice can be calculated using the mass flow rate and the velocity:
$Force = mass flow rate \times v$
The mass flow rate $˙ m$ can be expressed as:
$˙ m = ρ \cdot a \cdot v$
Thus, the force due to the efflux becomes:
$F = ˙ m \cdot v = ρ \cdot a \cdot v^{2}$
Substituting $v = \sqrt{2 g h}$ :
$F = ρ \cdot a \cdot (2 g h) = 2 ρ a g h$
Step 5: Apply Newton's Second Law
For the container to remain at rest, the frictional force must balance the force due to the efflux. The frictional force $F_{f}$ can be expressed as:
$F_{f} = μ \cdot N$
where $N$ is the normal force, which is equal to the weight of the fluid:
$N = ρ \cdot A \cdot h \cdot g$
Thus, we have:
$μ \cdot (ρ \cdot A \cdot h \cdot g) = 2 ρ a g h$
Step 6: Solve for the Coefficient of Friction
Now, we can simplify the equation:
$μ \cdot ρ \cdot A \cdot h \cdot g = 2 ρ a g h$
Dividing both sides by $ρ g h$ (assuming $ρ$ , $g$ , and $h$ are not zero):
$μ \cdot A = 2 a$
Thus, the coefficient of friction $μ$ is given by:
$μ = \frac{2 a}{A}$
Final Answer
The minimum coefficient of friction between the container and the ground so that the container does not move is:
$μ = \frac{2 a}{A}$

Updated on:7/8/2024

A wide tank of cross-section area A, containing a liquid to a height H, has an orifice at its base of area $\frac{A}{3}$ . The initial velocity of top surface of liquid is
A $\sqrt{\frac{g H}{4}}$
B $3 \sqrt{\frac{g H}{4}}$
C $\sqrt{\frac{g H}{2}}$
D $\frac{1}{3} \sqrt{\frac{g H}{2}}$
A cylindrical vessel of area of cross-section A is filled with water to a height H. It has capillary tube of length l and radius r fitted horizontally at its bottom. If the coeffiecient of viscosity of water is $η$ , then time required in which level will fall to a height $\frac{H}{2}$ is (density of water is $ρ$ )
A $\frac{η / r^{2}}{4 A ρ} 1 n (2)$
B $\frac{4 η / r^{4}}{π g A ρ} ln (\frac{1}{2})$
C $\frac{8 η / A}{ρ π g r^{4}} ln (2)$
D $\frac{4 H η / ρ}{π g r^{4}} ln (2)$
A cylindrical vessel of area of cross-section A and filled with liquid to a height of $h_{1}$ has a capillary tube of length l and radius r protuding horizontally at its bottom. If the viscosity of liquyid is $η$ and density $ρ$ . Find the time in which the level of water in the vessel falls to $h_{2}$ .
A $\frac{8 η l A}{π ρ g r^{4}}$ ln $\frac{h_{1}}{h_{2}}$
B $\frac{8 η l A}{π ρ g r^{4}}$
C $\frac{η A}{g} (\sqrt{h_{1}} - \sqrt{h_{2}})$
D $\frac{8 η l A}{π ρ g r^{4}}$ ln $\frac{h_{2}}{h_{1}}$