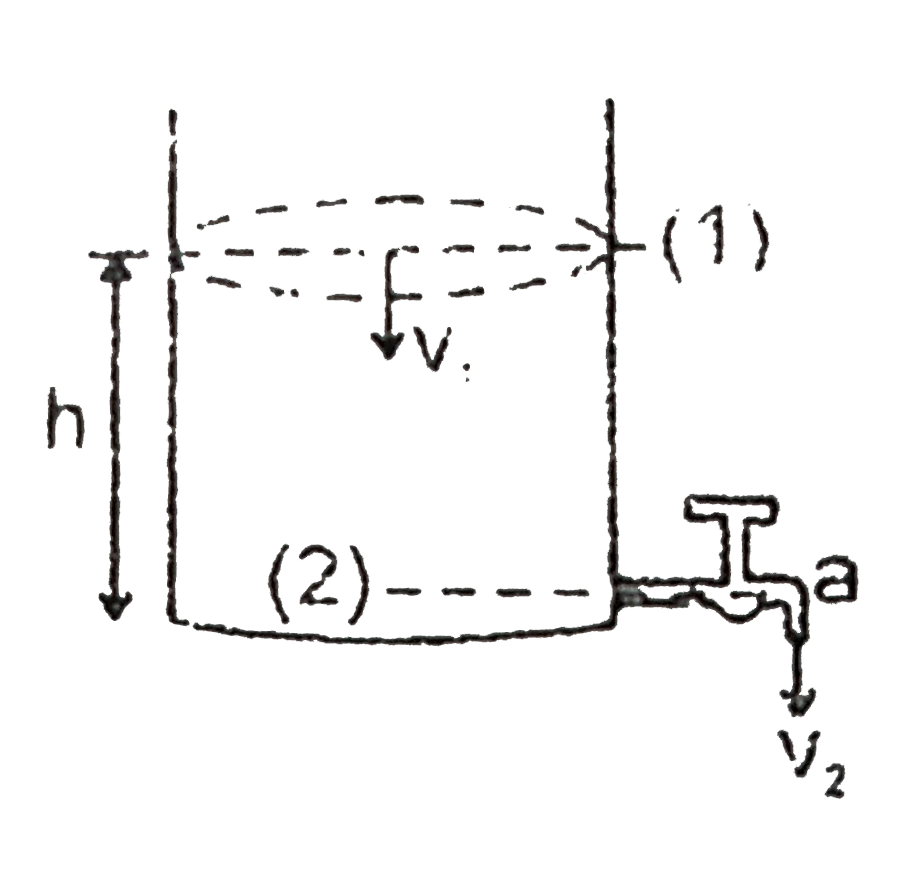
A cylindrical container of cross-section area, A is filled up with water upto height 'h' Water may exit through a tap of cross sectional area 'a' in the bottom of container. Find out

(a) Velocity of water just after opening of tap.
(b) The area of cross-section of water stream coming out of tape at depth h0 below tap in terms of 'a' just after opening of tap.
(c) Time in which conainer becomes empty.
(Given : (aA)1/2=0.22,h=20cm,h0=20cm
Applying Bernoulli's between (1) and (2).
Pa+ρgh+12ρv21=Pa+12ρv22
Through continuity equation :
Av1=av2,v1=av2aρgh+12ρv21=12ρv22
on solving - v2=
⎷2gh1−a2A2=2m/sec. .........(1)
(b) Appling Bernoulli's equation between (2) and (3)
12ρv22+ρgh0=12ρv23
Through continuity equation -
av2=a'v3⇒v3=av2a'
⇒12ρv22+ρgh0=12ρ(av2a')2

12×2×2+gh0=12(aa')2×2×2
(aa)2=1+9.8×.202⇒(aa')2=1.98⇒a'=a√1.98
(c) From (1) at any height 'h' of liquid level in container, the velocity through tap,
v=√2gh0.98=√20h
We know, volume of liquid coming out of tap = decrease in volume of liquid in container.
For any small ltime interval 'dt'
av2dt=−A⋅dx
a√20xdt=−Adx⇒t∫0dt=−Aa0∫hdx√20x
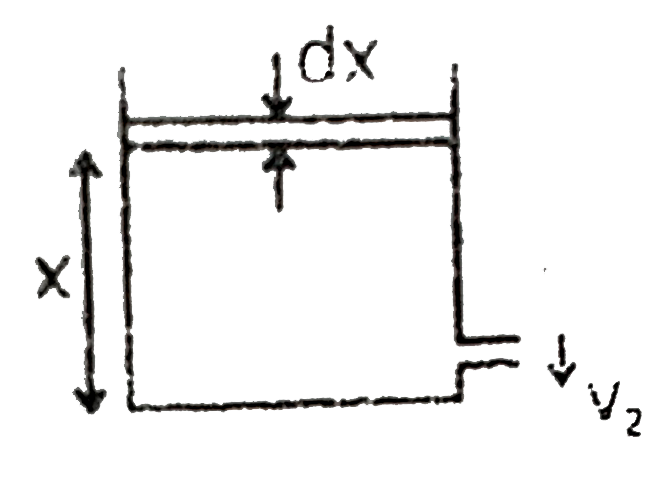
t=Aa√20[2√x]0h⇒t=Aa√202√h
=Aa×2×√h20=2Aa√0.2020=2Aa×0.1
Given (aA)1/2=0.2 or Aa=10.0004=2500
Thus t=2×2500×0.1=500 second.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise
18 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - I Section (A)
5 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Advanced Level Problems
8 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
A cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA cylindrical tank of cross sectional area a1 is filled with water to a height h. A hole of cross sectional area a2 is made at the bottom. If a1=5a2, then find the
(i) initial velocity with which the water falls in tank.
(ii) initial velocity with which water emerges out from hole.
(iii) time taken to make the tank empty.
View Solution
Knowledge Check
A cylindrical tank having cross-sectional area A is filled with water to a height of 2.0 m. A circular hole of corss-section area is opened at a height of 75 cm from the bottom. If a/A=√0.2, then velocity with which waer emerges from the hole is
(g=9.8ms−2)A4.9ms−1B4.95ms−1C5.0ms−1D5.5ms−1A hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2If water falls from a tap, then the volume rate of flow of water at depth of h, (A0 is the area of cross-section of the mouth and A02 is the corresponding area at depth h)
AA0√2ghBA0√23ghC2A0√ghDA0√3gh
A cylindrical massless container of cross sectional area A have a fluid filled up to height h and have a small orifice of area a in wall near its bottom. Find minimum coefficient between container and ground so that container does not move
View SolutionA cylindrical tank with a large diameter is filled with water to a depth D =0.30 m. A hole of cross-sectional area A = 6.2 cm2 in the bottom of the tank allows water to drain out. (a) What is the drainage rate in cubic meters per second? (b) At what distance below the bottom of the tank is the cross-sectional area of the stream equal to one half the area of the hole?
View SolutionIn the previous question, at the mouth of the tap the area of cross-section is 2.5cm2 and the speed of water in 3m/s. The area of cross-section of the water column 80cm below the tap is.
View SolutionA cylindrical vessel of cross section A contains water to a height h. There is a hole in the bottom of radius 'a'. The time in which it will be emptied is:
View SolutionA large cylindrical tank has a hole of area A at its bottom. Water is oured in the tank by a tube of equal cross sectional area A ejecting water at the speed v.
View Solution
