Two masses on 1kg each are rotating in a circle of radius R under their gravitational force. Find their angular speed in terms of G and R
To find the angular speed of two masses each of 1 kg rotating in a circle of radius R under their gravitational force, we can follow these steps:
Step 1: Understand the System
We have two masses, m1 and m2, each with a mass of 1 kg. They are rotating in a circular path with a radius R. The distance between the two masses is 2R since they are on opposite sides of the circle.
Step 2: Write the Gravitational Force
The gravitational force F between the two masses is given by Newton's law of gravitation:
F=Gm1m2d2
where G is the gravitational constant, m1=1kg, m2=1kg, and d=2R (the distance between the two masses).
Substituting the values, we have:
F=G⋅1⋅1(2R)2=G4R2
Step 3: Relate Gravitational Force to Centripetal Force
For circular motion, the gravitational force provides the necessary centripetal force. The centripetal force Fc required for one mass is given by:
Fc=mv2R
where m is the mass (1 kg) and v is the tangential speed.
Step 4: Express Tangential Speed in Terms of Angular Speed
The tangential speed v can be expressed in terms of angular speed ω:
v=Rω
Substituting this into the centripetal force equation gives:
Fc=1⋅(Rω)2R=Rω2
Step 5: Set Gravitational Force Equal to Centripetal Force
Now, we set the gravitational force equal to the centripetal force:
G4R2=Rω2
Step 6: Solve for Angular Speed ω
Rearranging the equation to solve for ω2:
ω2=G4R3
Taking the square root gives:
ω=√G4R3
Final Answer
Thus, the angular speed ω in terms of G and R is:
ω=√G4R3
We have two masses, m1 and m2, each with a mass of 1 kg. They are rotating in a circular path with a radius R. The distance between the two masses is 2R since they are on opposite sides of the circle.
The gravitational force F between the two masses is given by Newton's law of gravitation:
F=Gm1m2d2
where G is the gravitational constant, m1=1kg, m2=1kg, and d=2R (the distance between the two masses).
F=G⋅1⋅1(2R)2=G4R2
For circular motion, the gravitational force provides the necessary centripetal force. The centripetal force Fc required for one mass is given by:
Fc=mv2R
where m is the mass (1 kg) and v is the tangential speed.
The tangential speed v can be expressed in terms of angular speed ω:
v=Rω
Substituting this into the centripetal force equation gives:
Fc=1⋅(Rω)2R=Rω2
Now, we set the gravitational force equal to the centripetal force:
G4R2=Rω2
Rearranging the equation to solve for ω2:
ω2=G4R3
Taking the square root gives:
ω=√G4R3
Thus, the angular speed ω in terms of G and R is:
ω=√G4R3
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Four particles of equal mass are moving round a circle of radius r due to their mutual gravitational attraction . Find the angular velocity of each particle .
View SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
Two identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is :
A√G2R3B12√GR3C12R√1GD√2GR3Four masses 'm' each are orbitinting in a circular of radius r in the same direction under gravitational force. Velocityof each particle is
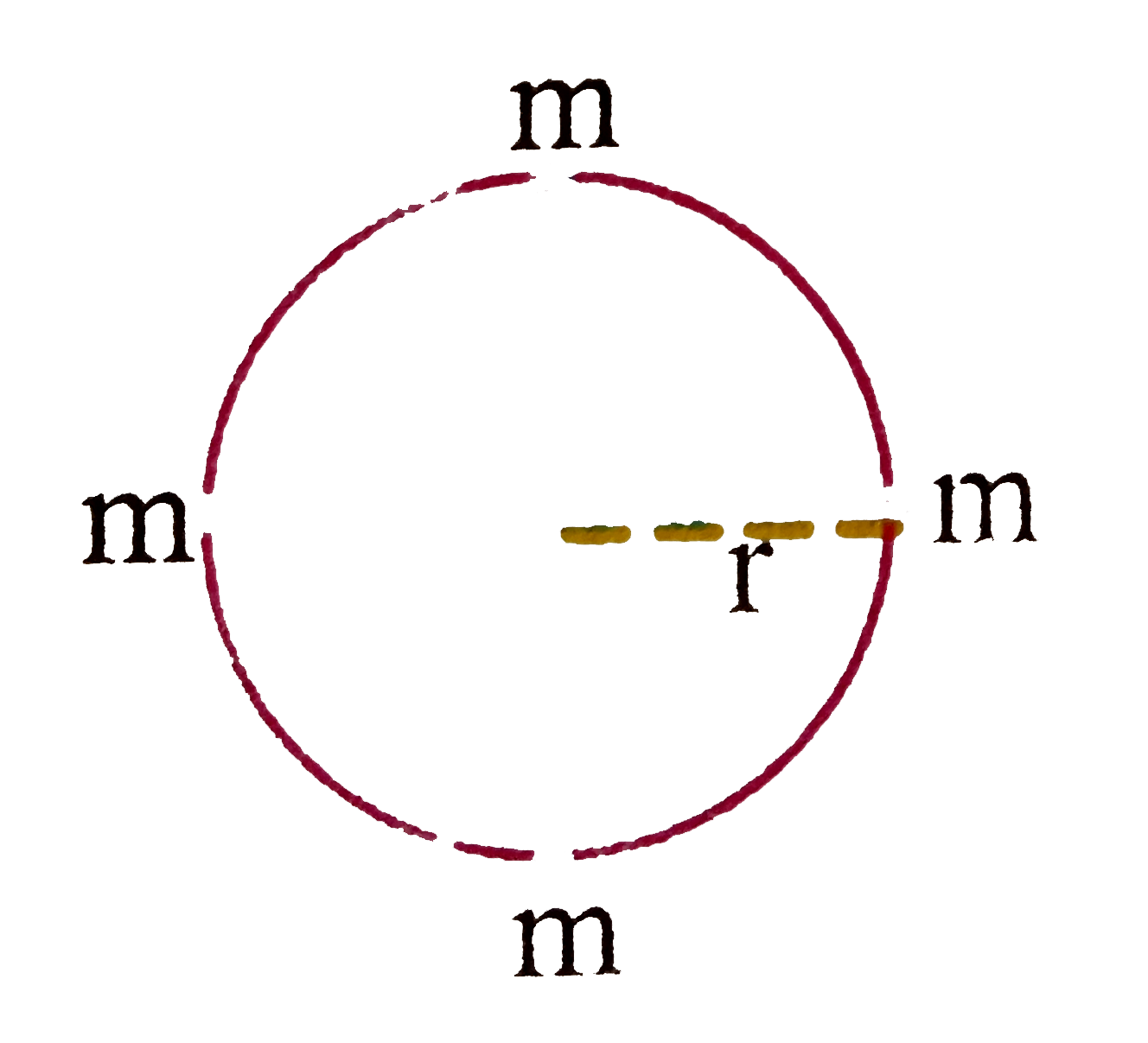 A ⎷Gmr(1+2√2)2B√GmrC√Gmr(1+2√2)D ⎷Gm2r(1+2√22)
A ⎷Gmr(1+2√2)2B√GmrC√Gmr(1+2√2)D ⎷Gm2r(1+2√22)Three particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
A√GM√2RB√GM√3RC√GM2RD√GM3R
Two charges +qand−q, each of mass m, are revoloving in a circle of radius R, under mutal electrostatic force, Find (i) speed of each charge (ii) kinitic energy of the system (iii) potental energy of the system and (iv) total energy of the system.
View SolutionFor particles of equal massses M move along a circle of radius R under th action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo charges +qand−q, each of mass m, are revoloving in a circle of radius R, under mutal electrostatic force, Find (i) speed of each charge (ii) kinitic energy of the system (iii) potental energy of the system and (iv) total energy of the system.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View Solution
