Constant power p is supplied by engine to mass m displacement of mass after time t will be
To solve the problem of finding the displacement of a mass m under constant power P after a time t, we can follow these steps:
1. Understanding Power and Work Done:
The power P supplied by the engine is defined as the rate of doing work. The work done W over a time t can be expressed as:
W=P⋅t
2. Relating Work to Kinetic Energy:
Since the mass starts from rest, all the work done by the engine goes into increasing the kinetic energy of the mass. The kinetic energy KE of the mass m is given by:
KE=12mv2
Therefore, we can set the work done equal to the change in kinetic energy:
P⋅t=12mv2
3. Expressing Velocity in Terms of Power:
Rearranging the equation for velocity v:
v2=2Ptm
Taking the square root gives:
v=√2Ptm
4. Using the Relationship Between Velocity and Displacement:
The velocity v can also be expressed as the derivative of displacement x with respect to time t:
v=dxdt
Substituting for v:
dxdt=√2Ptm
5. Separating Variables and Integrating:
Rearranging gives:
dx=√2Pm⋅√tdt
Now we integrate both sides. The limits for t will be from 0 to t and for x from 0 to x:
∫x0dx=√2Pm∫t0√tdt
6. Calculating the Integral:
The integral of √t is:
∫√tdt=23t3/2
Evaluating from 0 to t:
∫t0√tdt=23t3/2
7. Substituting Back:
Therefore, we have:
x=√2Pm⋅23t3/2
Simplifying gives:
x=2√2P3√mt3/2
Final Result:
The displacement x of the mass after time t is:
x=2√2P3√mt3/2
The power P supplied by the engine is defined as the rate of doing work. The work done W over a time t can be expressed as:
W=P⋅t
Since the mass starts from rest, all the work done by the engine goes into increasing the kinetic energy of the mass. The kinetic energy KE of the mass m is given by:
KE=12mv2
Therefore, we can set the work done equal to the change in kinetic energy:
P⋅t=12mv2
Rearranging the equation for velocity v:
v2=2Ptm
Taking the square root gives:
v=√2Ptm
The velocity v can also be expressed as the derivative of displacement x with respect to time t:
v=dxdt
Substituting for v:
dxdt=√2Ptm
Rearranging gives:
dx=√2Pm⋅√tdt
Now we integrate both sides. The limits for t will be from 0 to t and for x from 0 to x:
∫x0dx=√2Pm∫t0√tdt
The integral of √t is:
∫√tdt=23t3/2
Evaluating from 0 to t:
∫t0√tdt=23t3/2
Therefore, we have:
x=√2Pm⋅23t3/2
Simplifying gives:
x=2√2P3√mt3/2
The displacement x of the mass after time t is:
x=2√2P3√mt3/2
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A constant power P is applied on a particle of mass m. find kinetic energy, velocity and displacement of particle as function of time t.
View SolutionParticle sticks to wooden loop, If particle reach at the lowest position for first time after time T. Then displacement of centre of mass of system in this time interval will be :

View Solution
Knowledge Check
An automobile engine of mass m accelerates and a constant power P is applied by the engine. The instantaneous speed of the engine will be
Apt2mB2ptmC(pt2m)1/2D(2ptm)1/2An automobile engine of mass m accelerates and a constant power Pis applied by the engine. The instantaneous speed of the engine will be
APt2mB2PtmC(Pt2m)12D(2Ptm)12A car of mass M accelerates starting from rest. Velocity of the car is given by v=(2PtM)12 where P is the constant power supplied by the engine. The position of car as a function of time is given as
A(8P9M)12t32B(9P8M)12t32C(8P9M)12t23D(9P8M)t3
A block is pulled with constant power what is the relation between displacement(x) and time(t) for this
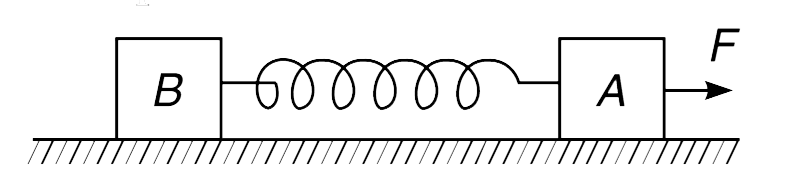
View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
View SolutionConstant power P is supplied to a particle having mass m and initially at rest. choose correct graph.
View SolutionA particle of mass m moves in a circular path of radius r, under the action of force which delivers it constant power p and increases its speed. The angular acceleration of particle at time (t) is proportional
View Solution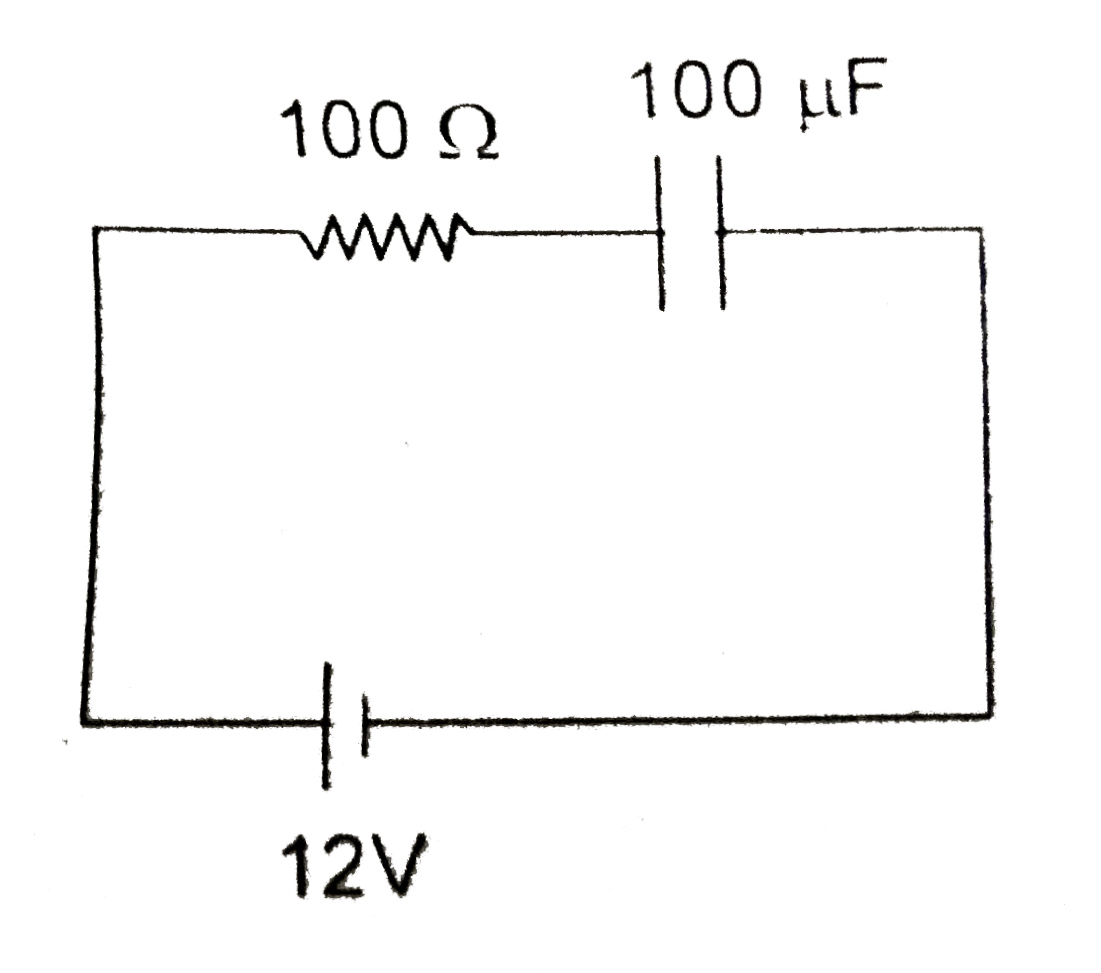
The value of displacement current at t=1 time constant is
View Solution
