Particle sticks to wooden loop, If particle reach at the lowest position for first time after time T. Then displacement of centre of mass of system in this time interval will be :

√(uT2)2+R2
√(uT)2+R2
12√(uT)2+R2
None of these
NA
Topper's Solved these Questions
Similar Questions
A particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=0 s to t=1 s.
View Solution
Knowledge Check
If the displacement of a particle varies with time as √x=t+3
Avelocity of the particle is inversely proportional to tBvelocity of particle varies linearly with tCvelocity of particle is proportional to √tDinitial velocity of the particle is zeroA particle on the trough of a wave at any instant will come to the mean position after a time ( T = time period)
AT/2BT/4CTD2TIf the displacement of a particle is proportional to the square of time, then-
Avelocity is inversely proportional to tBvelocity is proportional to tCvelocity is proportional to√tDacceleration is constant
The position of a particle varies with function of time as y=(4sint+3cost)m. Then the maximum displacement of the particle from origin will be
View SolutionThe position of a particle moving along the straight line is given as s= (t^(2)-4t+3)m where t is time in s .The magnitude of displacement of the particle during time interval t=0 to till its velocity becomes zero
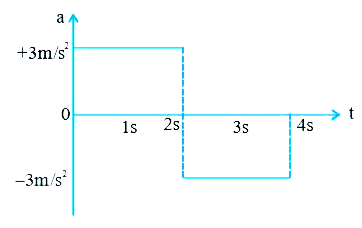
View SolutionA particle starts from rest at t=0 and undergoes an acceleration as shown in figure.
Draw the displacement-time graph of the motion of the particle during the same time interval. In both the above cases, explain the various steps.
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionA particle is in SHM with time period 3 sec. Calculate the displacement of particle from mean position after t = 0.5 sec.
View Solution
