If A:B=1:2,B:C=3:4,C:D=6:9 and D:E=12:16 then A:B:C:D:E is equal to
1:3:6:12:16
2:4:6:9:16
3:4:8:12:16
3:6:8:12:16
The correct Answer is:D
To solve the problem of finding the ratio A:B:C:D:E given the individual ratios, we can follow these steps:
Step 1: Write down the given ratios
We have the following ratios:
1. A:B=1:2
2. B:C=3:4
3. C:D=6:9
4. D:E=12:16
Step 2: Express each variable in terms of a common variable
Let's express each variable in terms of A:
- From A:B=1:2, we can say B=2A.
- From B:C=3:4, substituting B gives 2A:C=3:4. Therefore, C=43×2A=83A.
- From C:D=6:9, substituting C gives 83A:D=6:9. Therefore, D=96×83A=123A=4A.
- From D:E=12:16, substituting D gives 4A:E=12:16. Therefore, E=1612×4A=43×4A=163A.
Step 3: Write down all variables in terms of A
Now we have:
- A=A
- B=2A
- C=83A
- D=4A
- E=163A
Step 4: Find a common denominator to combine the ratios
To combine these ratios, we can find a common denominator. The denominators we have are 1,2,83,4,163. The least common multiple of the denominators 1,2,3,4 is 12.
Step 5: Convert each ratio to have the same denominator
Now we convert each variable:
- A=12
- B=2A=2×12=24
- C=83A=83×12=32
- D=4A=4×12=48
- E=163A=163×12=64
Step 6: Write the final ratio
Thus, the final ratio A:B:C:D:E is:
A:B:C:D:E=12:24:32:48:64
Step 7: Simplify the ratio
To simplify this ratio, we can divide each term by 4:
A:B:C:D:E=3:6:8:12:16
Final Answer:
Thus, the ratio A:B:C:D:E is equal to 3:6:8:12:16.
---
We have the following ratios:
1. A:B=1:2
2. B:C=3:4
3. C:D=6:9
4. D:E=12:16
Let's express each variable in terms of A:
- From A:B=1:2, we can say B=2A.
- From B:C=3:4, substituting B gives 2A:C=3:4. Therefore, C=43×2A=83A.
- From C:D=6:9, substituting C gives 83A:D=6:9. Therefore, D=96×83A=123A=4A.
- From D:E=12:16, substituting D gives 4A:E=12:16. Therefore, E=1612×4A=43×4A=163A.
Now we have:
- A=A
- B=2A
- C=83A
- D=4A
- E=163A
To combine these ratios, we can find a common denominator. The denominators we have are 1,2,83,4,163. The least common multiple of the denominators 1,2,3,4 is 12.
Now we convert each variable:
- A=12
- B=2A=2×12=24
- C=83A=83×12=32
- D=4A=4×12=48
- E=163A=163×12=64
Thus, the final ratio A:B:C:D:E is:
A:B:C:D:E=12:24:32:48:64
To simplify this ratio, we can divide each term by 4:
A:B:C:D:E=3:6:8:12:16
Thus, the ratio A:B:C:D:E is equal to 3:6:8:12:16.
Topper's Solved these Questions
- RATIO AND PROPORTION BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-IV
30 Videos
- RATIO AND PROPORTION BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-V
64 Videos
- RATIO AND PROPORTION BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-II
49 Videos
- PROFIT AND LOSS BOOK - KIRAN PUBLICATIONCHAPTER - PROFIT AND LOSS EXERCISE - TEST YOURSELF
23 Videos
- SEQUENCE AND SERIES BOOK - KIRAN PUBLICATIONCHAPTER - SEQUENCE AND SERIES EXERCISE - TEST YOURSELF
20 Videos
Similar Questions
Knowledge Check
If a:b=c:d=e:f=1:2, then ( 3a + 5c +7e): (3b + 5d + 7 J) is equal to
A8:7B2:1C1:4D1:2If A={a,b,c,d}andB={b,c,e}, then A∪B is equal to
A{a,b,c,d,e}BϕC{b,c,d}DNone of theseIf a, b, c, d, e, f are A.M's between 2 and 12, then a + b + c + d + e + f is equal to
A14B42C84Dnone of these
If A:B=3:4,B:C=8:9,C:D=15:16 then A:D is equal to ?
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
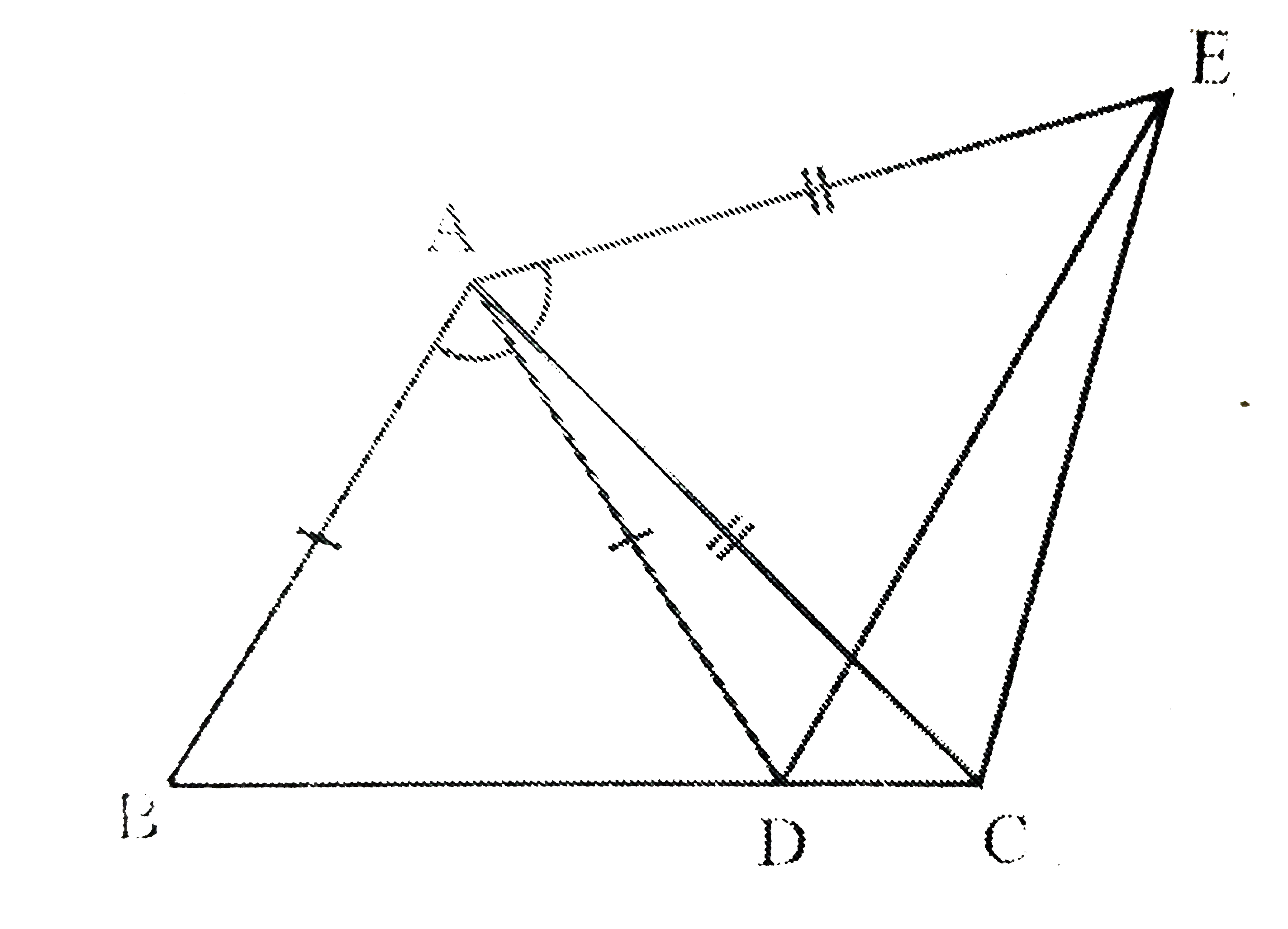
View SolutionIf A:B=12:13na dB:C=12:13, then A:B:C is equal to 1:2:6 b. 3:2:6 c. 2:3:3 d. 9:6:4
View SolutionIf a;b=c:d=e:f=1:2, then (3a+5c+7e):(3b=5d+7f) 1:2 b. 1:4 c. 2:1 d. 8:7
View SolutionIf A={a,b,c,d}andB={b,c,e}, then A∪B is equal to
View Solution
