Marks of two candidates P and Q are in the ratio of 2:5. If the marks of P is 120, marks of Q will be:
120
240
300
360
The correct Answer is:C
To solve the problem, we need to find the marks of candidate Q given that the marks of candidates P and Q are in the ratio of 2:5, and that candidate P has scored 120 marks.
1. Understand the Ratio: The ratio of marks of P to Q is given as 2:5. This means for every 2 parts of marks that P has, Q has 5 parts.
2. Assign Variables: Let the marks of P be represented as 2x and the marks of Q as 5x, where x is a common multiplier.
3. Set Up the Equation: We know from the problem that the marks of P are 120. Therefore, we can set up the equation:
2x=120
4. Solve for x: To find the value of x, divide both sides of the equation by 2:
x=1202=60
5. Calculate Marks of Q: Now that we have the value of x, we can find the marks of Q using the expression 5x:
Marks of Q=5x=5×60=300
6. Conclusion: Therefore, the marks of candidate Q are 300.
Final Answer:
The marks of candidate Q will be 300.
---
2x=120
x=1202=60
Marks of Q=5x=5×60=300
The marks of candidate Q will be 300.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-IV30videos
RATIO AND PROPORTION
- BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-V64videos
RATIO AND PROPORTION
- BOOK - KIRAN PUBLICATIONCHAPTER - RATIO AND PROPORTION EXERCISE - TYPE-II49videos
RATIO AND PROPORTION
- BOOK - KIRAN PUBLICATIONCHAPTER - PROFIT AND LOSS EXERCISE - TEST YOURSELF23videos
PROFIT AND LOSS
- BOOK - KIRAN PUBLICATIONCHAPTER - SEQUENCE AND SERIES EXERCISE - TEST YOURSELF20videos
SEQUENCE AND SERIES
Similar Questions
The average of marks obtained by 120 candidates in a certain examination is 35. If the average marks of passed candidates is 39 and that of the failed candidates is 15, what is the number of candidates who passed the examination?
View SolutionIn an examination, six subjects - S1, S2, S3, S4, S5, and S6 have equal maximum marks. The number of marks scored by one particular candidate in subject S1 is 20% less than his marks in subject S6. The ratio of marks scored by the same candidate in subject S2 to that in S3 is 4: 5 and that in S4 to S5 is 3: 4. The number of marks scored by this candidate in subject S5 is 25% more than that of S6. He scored 65 marks in the subject S3. He scored 436/9 % in the examination and the average of marks scored by him in all the subjects is 218/3
What percentage of marks the candidate had scored in the subject S5 over the maximum marks of that subject?View Solution
Knowledge Check
- Question 1 - Select One
Marks of two candidates P and Q are in the ratio of 2:5. If the marks of P are 12, marks of Q are
A120B240C300D360 - Question 2 - Select One
Marks of two candidates X and Y are in the ratio of 4 : 7. If the marks of X is 140, then what will be the marks of Y?
A210B180C245D225 - Question 3 - Select One
Find the class mark of the class 90−120.
A100B101C104D105
The line chart given below shows the marks scored by 2 students P and Q in five subjects.
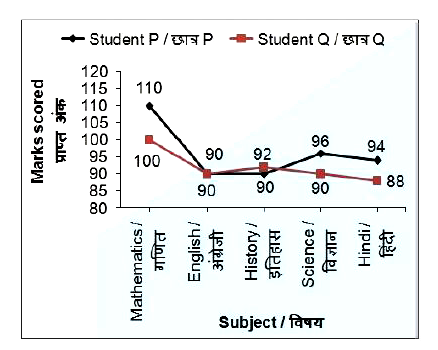
What is the ratio of the marks scored by student P in Science to the marks scored by student Q in History?View SolutionThe average marks obtained by 22 candidates in an examination are 45. The average marks of the first 10 candidates are 55 and those of the last eleven are 40. The number of marks obtained by the eleventh candidate is:
View SolutionA candidate needs 35% marks to pass. If he gets 96 marks and fails by 16 marks. Then maximum marks are -
View SolutionThe bar chart given below shows the marks obtained by P and Q in 5 tests. The maximum marks for each test in 200.
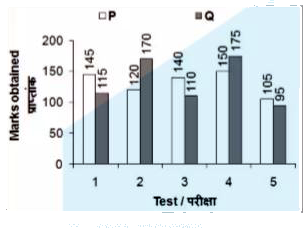
The marks obtained by P in test 3 is how much percent more than the marks obtained in test 2?View SolutionThe average marks obtained by 22 candidates in an examination are 45. The average marks of the first 10 candidates are 55 and those of the last eleven are 40. The number of marks obtained by the eleventh candidate is:
View Solution

