In an isosceles triangle PQR, ∠P=130∘. If I is the in-centre of the triangle, what is the value (in degrees) of ∠QIR?
130
120
155
165
The correct Answer is:C
To find the value of angle ∠QIR in the isosceles triangle PQR where ∠P=130∘, we can follow these steps:
Step 1: Determine the angles ∠Q and ∠R
Since triangle PQR is isosceles with ∠P=130∘, the other two angles ∠Q and ∠R must be equal. We know that the sum of angles in a triangle is 180∘.
∠P+∠Q+∠R=180∘
130∘+∠Q+∠Q=180∘
130∘+2∠Q=180∘
2∠Q=180∘−130∘
2∠Q=50∘
∠Q=25∘
∠R=25∘
Step 2: Use the property of the incenter
The incenter I of a triangle is the point where the angle bisectors of the triangle intersect. The angle ∠QIR can be calculated using the formula:
∠QIR=12(∠Q+∠R)
Step 3: Substitute the values of ∠Q and ∠R
Since ∠Q=25∘ and ∠R=25∘:
∠QIR=12(25∘+25∘)
∠QIR=12(50∘)
∠QIR=25∘
Step 4: Calculate ∠QIR
To find ∠QIR in terms of ∠P:
Using the property of the incenter, we can also express it as:
∠QIR=90∘+∠P2
Substituting ∠P=130∘:
∠QIR=90∘+130∘2
∠QIR=90∘+65∘
∠QIR=155∘
Final Answer
Thus, the value of ∠QIR is 155∘.
---
130∘+∠Q+∠Q=180∘
130∘+2∠Q=180∘
2∠Q=180∘−130∘
2∠Q=50∘
∠Q=25∘
∠R=25∘
∠QIR=12(50∘)
∠QIR=25∘
∠QIR=90∘+65∘
∠QIR=155∘
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)109videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)35videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
In an isosceles triangle DEF,∠D=110∘. If I is the in centre of the triangle, then what is the value (in degrees) of ∠EIF?
A110B130C145D155 - Question 2 - Select One
In an isosceles triangle DEF,∠D=110∘. If I is the in centre of the triangle, then what is the value (in degrees) of ∠EIF?
A110B130C145D155 - Question 3 - Select One
Triangle PQR is inscribed in a circle such that P Q and R lie on the circumference. If PQ is the diameter of the circle and ∠PQR=40∘, then what is the value (in degree) of QPR?
A40B45C50D55
In an isosceles right triangle PQR, if ∠Q=90∘, then find ∠PRQ.
View SolutionIn an isosceles right triangle PQR, if ∠Q=90∘, then find ∠PRQ.
View SolutionIn △PQR, I is the incentre of the triangle. If ∠QIR=107∘,then what is the measure of ∠P?
त्रिभुज PQR में, I त्रिभुज का अंतःकेंद्र है | यदि ∠QIR=107∘ है, तो कोण P का माप कया है?View SolutionI is the incentre of a triangle PQR and ∠=107∘ then find the value ∠P.
View SolutionIn the given figure, PQRS is a square and SRT is an equliateral triangle. What is the value (in digrees) of ∠SOR ?
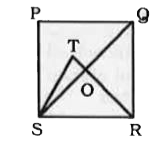 View Solution
View Solution