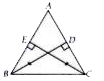
In ΔABC,BDandCEareperpendica––r→ACandABrespectively.IfBD = CE,thenDelta ABC is
Equilateral
Isosceles
Right-angled
Scalene
The correct Answer is:B
To solve the problem, we need to analyze the given information about triangle ABC and the perpendiculars BD and CE.
1. Understand the Triangle Configuration:
We have triangle ABC, where BD is perpendicular to AC and CE is perpendicular to AB.
2. Identify the Lengths of the Perpendiculars:
We are given that BD = CE. This means the heights from points D and E to the respective bases AC and AB are equal.
3. Use the Property of Triangles:
In any triangle, if two heights (altitudes) from different vertices to their respective bases are equal, then the bases must also be equal for the triangle to maintain its shape.
4. Conclusion about the Triangle:
Since BD = CE and they are the heights from points B and C to sides AC and AB respectively, it follows that the lengths of the bases AC and AB must be equal. Therefore, triangle ABC is an isosceles triangle.
Final Answer:
Triangle ABC is an isosceles triangle.
---
We have triangle ABC, where BD is perpendicular to AC and CE is perpendicular to AB.
We are given that BD = CE. This means the heights from points D and E to the respective bases AC and AB are equal.
In any triangle, if two heights (altitudes) from different vertices to their respective bases are equal, then the bases must also be equal for the triangle to maintain its shape.
Since BD = CE and they are the heights from points B and C to sides AC and AB respectively, it follows that the lengths of the bases AC and AB must be equal. Therefore, triangle ABC is an isosceles triangle.
Triangle ABC is an isosceles triangle.
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)
109 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)
35 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
In Δ ABC, DE || AC, D and E are two points on AB and CB respectively, If AB=10 cm and AD =4 cm, then BE : CE is
A2:3B2:5C5:2D3:2If in △ABC, D and E are the points on sides AC and BC, respectively such that DE || AB. F is the point on CE such that DF ||AE. If CE= 6cm and CF = 2.5 cm, then BC is equal to:
त्रिभुज ABC में, D और E क्रमशः भुजाओं AC तथा BC के मध्य बिंदु हैं जो इस प्रकार ह कि DE || AB है F, CE पर स्थित ऐसा बिंदु है कि DF|| AE है | यदि CE= 6 सेमी और CF =2.5 सेमी है, तो BC किसके बराबर है ?A12 cmB15.6 cmC14 cmD14.4 cmAn isosceles triangle ABC is right angled at B.D is a point inside the triangle ABC. P and Q are the feet of the perpendiculars drawn from D on the sides AB and AC respectively of ΔABC. If AP = a cm, AQ = b cm and ∠BAD=15∘,sin75∘=
A2b√3aBa2bC√(3)(a)2bD2a√3b
ABC is an equilateral triangle, and AD and BE are perpendiculars to BC and AC respectively. Prove that: 1. AD=BE 2. BD=CE [ΔABD=ΔBCE.]
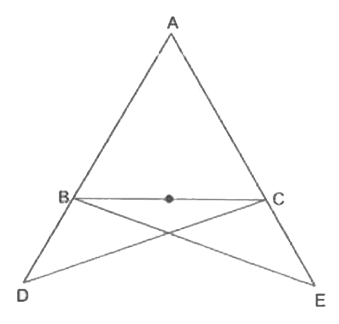
View SolutionIn the given figure, △ABC is an isosceles triangle in which AB - AC. If AB and AC are produced to D and E respectively such that BD = CE, prove that BE = CD. Hint. Show that △ACD=△ABE.
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DEBC.
View SolutionIn a ABC, BD and CE are the altitudes. Prove that ADB and AEC are similar. Is CDBBEC ?
View SolutionIf D and E are points on sides AB and AC respectively of a ABC such that DEBC and BD=CE . Prove that ABC is isosceles.
View Solution